در بسیاری از سیستمهای کنترل سیگنالهای مزاحمی به نام اغتشاش وجود دارند که عملکرد حلقه بسته را تحت تاثیر قرار میدهند و عموما ما اطلاع چندانی از ماهیت آنها نداریم. تنها چیزی که از آنها میدانیم این است که دارای انرژی محدود هستند و بینهایت نیستند. یکی از روشهای پرکاربرد و مفید برای تضعیف این اغتشاشات کنترل مقاوم ∞H است. متاسفانه برای حل مساله تضعیف اغتشاش با استفاده از روش ∞H (با دستورات آماده متلب) باید سیستم حلقه باز را به شکل استاندارد موجود در تئوری ∞H دربیاورید تا بتوانید از تولباکس آماده متلب استفاده کنید. این کار مستلزم مطالعه پیشنیازهای فراوان ریاضی و مطالعه کل تئوری ∞H است. خوشبختانه راههای سادهتری برای این مساله وجود دارد. در این سری جلسات مساله تضعیف اغتشاش را با استفاده از نامساوی های ماتریسی خطی یا LMI خدمت شما تقدیم میکنم. کل مبحث طی چهار جلسه خلاصه شده و LMI های مورد نیاز برای محاسبه بهره کنترل کننده فیدبک حالت بدست آمده است. کسانی که به اثبات قضیه علاقمند نباشند کافی است که ماتریسهای سیستم مورد نظرشان را داخل کد ارائه شده قرار بدهند و بهره کنترل کننده فیدبک حالت مقاوم را بدست آورند. کسانی هم که دوست دارند بیشتر عمیق بشوند، میتوانند اثبات کامل پایداری را به روش مستقیم لیاپونوف که در جلسه دوم ارائه شده، ملاحظه کنند. با امید به اینکه مورد رضایت شما عزیزان قرار بگیرد…
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
معرفی مفاهیم پایه Passivity، Dissipativity و L2-gain Stability و ارتباط با روش ∞H
در این جلسه ابتدا برخی توضیحات کلی در مورد کنترل مقاوم ارایه شده و روشهای متفاوت موجود در این حوزه معرفی میشوند. همچنین مزایای استفاده از نامساویهای ماتریسی خطی برای حل مساله کنترل مقاوم نسبت به روشهای مرسوم مانند ∞H بیان میشود. در ادامه تعریف سیستمهای تلف کننده (dissipative) و دو زیر مجموعه مهم آن یعنی سیستمهای پسیو (passive) و پایدار بهره ال2 (L2-gain stable) بحث شده و رابطه بین این مفاهیم پایداری بیان میشود. در انتها ارتباط انواع پایداری در حالت خاص سیستمهای خطی با نرم ∞H سیستم مطرح شده و مفهوم تضعیف اغتشاش با این نرم بر اساس کتاب غیرخطی خلیل تشریح میشود.
مدت زمان آموزش: 70 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و کتاب کنترل غیرخطی خلیل
پیش نمایش جلسه اول:
جلسه دوم:
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
در این جلسه با توجه به مقدمات ذکر شده در جلسه قبل و با استفاده از تئوری پایداری لیاپونوف شرط نامساوی ماتریسی خطی برای تضمین تضعیف اغتشاش محاسبه میگردد. برای این کار برخی از ترفندهای LMI مانند تبدیل متجانس (congruent transformation) و schur complement مورد استفاده قرار میگیرد. همچنین نحوه فراهم سازی پارامترهای آزاد و بهره L2 سیستم برای حل LMI تشریح میشود.
مدت زمان آموزش: 68 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و مقاله مورد اشاره در فیلم
پیش نمایش جلسه دوم:
جلسه سوم:
پیادهسازی کنترلکننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیهسازی در متلب
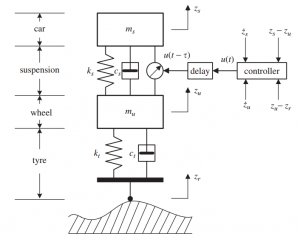
در این جلسه روش تضعیف اغتشاش بدست آمده در جلسه قبل بر روی یک مدل یک چهارم سیستم تعلیق فعال خودرو پیاده شده است. لازم به ذکر است که تمامی LMI ها با استفاده از تولباکس YALMIP در محیط متلب حل شده اند و بنابراین شما باید این تولباکس را قبل از اجرای کدها بر روی متلب نصب کرده باشید. برای توضیحات تکمیلی درباره نحوه دانلود و نصب تولباکس YALMIP به جلسه ششم از سری فیلمهای آموزش حل ناتساویهای ماتریسی خطی مراجعه فرمایید. همچنین نحوه تعیین خروجی رگوله شده (penalty vector) برای سیستم تعلیق و ماتریسهای آزاد برای طراحی کنترل کننده مقاوم تشریح شده است. بعد از طراحی کنترل کننده فیدبک حالت، سیستم حلقه بسته برای دو حالت فعال و غیر فعال شبیه سازی شده و نتایج باهم مقایسه شده اند. نتایج شبیهسازی نشاندهنده عملکرد مطلوب کنترل کننده مقاوم در برابر انواع مختلف پروفایل جاده نسبت به کنترل غیر فعال است.
مدت زمان آموزش: 71 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس – کدهای متلب مربوط به طراحی و شبیهسازی و مقاله مورد استفاده در طراحی و شبیهسازی
پیش نمایش جلسه سوم:
جلسه چهارم:
حل مساله ردیابی برای سیستمهای دارای اغتشاش خارجی
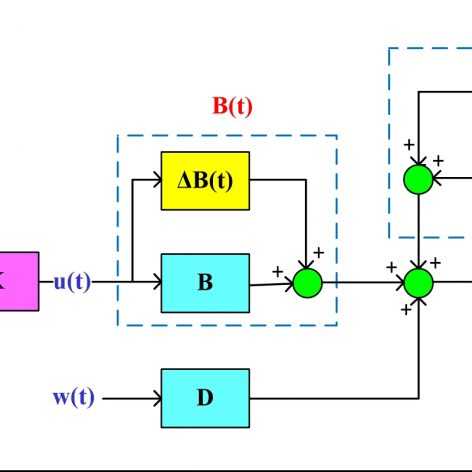
در این جلسه ابتدا قانون کلی ردیابی برای سیستمهای خطی و به خصوص برای سیستم خطی دارای اغتشاش خارجی استخراج شده و ساختار کنترل کننده مقاوم فیدبک حالت که به طور همزمان قادر به حل مساله تضعیف اغتشاش و ردیابی است؛ معرفی میشود. در ادامه روش فوق برای سیستم تعلیق فعال که در جلسه پیش مساله رگولاسیون برای آن حل شده بود؛ اعمال شده و کنترل کننده مورد نظر بر روی سیستم تعلیق اعمال شده و عملکرد آن مورد ارزیابی قرار میگیرد. همچنین اثر سیگنال مرجع با فرکانس های متفاوت نیز روی حالتهای سیستم طی شبیهسازیهای مختلف بررسی میشود.
مدت زمان آموزش: 66 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و کدهای متلب مربوط به طراحی و شبیهسازی
حجم فایل: 105 مگابایت
پیش نمایش جلسه چهارم:
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



محمد طالبی ( مالک تایید شده )
سلام و وقت بخیر
آیا می شود از روش LMI برای سیستم های غیرخطی استفاده کرد؟ اگر به طور مستقیم نمی شود؛ ممکنه در هر گام زمانی سیستم حول نقطه فعلی اش خطی شود و سپس از تئوری مربوط به سیستم های خطی استفاده شود؟
مدیر سایتادمین سایت
سلام
برای سیستمهای غیرخطی معمولا از جملات دارای شرط لیپشیتز یا sector bounded استفاده میشه و براش LMI های مربوطه محاسبه میشه.
برای مثال به مقاله زیر مراجعه کنید:
https://www.tandfonline.com/doi/abs/10.1080/00207721.2017.1367048
البته در این مقاله این روش برای سیستمهای تصادفی دارای تاخیر اعمال شده.
با خطی سازی چند زیر سیستم خطی تولید میشه که باید روشهای مربوط به سیستمهای سویچینگ روش اعمال بشه
negar sheykhi
سلام فایل خریداری شده با لینک ارسال شده باز نمیشود
م.ک
با سلام و خسته نباشید
خواستم بدونم توی سایت آموزشی برای رسم دیاگرام بود سیستم کنترلی که اینجا تدریس کردین وجود داره؟
البته نمیخوام توی محیط simulink باشه دنبال یه روش ساده هستم
دکتر علی جوادی
سلام
با دستور bode رسم کنید
م.ک
آخه استاد ما دوتا ورودی داریم چطور براش تابع تبدیلشو محاسبه کنیم؟
میشه مثل وقتی که شما میخواستین کنترلر رو طراحی کنین تبدیلش کنیم به open loop یعنی نیروی کنترلی رو ببریم تو ماتریس سیستم و ورودیمونم فقط اغتشاش باشه
دکتر علی جوادی
وقتی دو ورودی داشته باشید، یعنی دو تابع تبدیل و بنابراین دو دیاگرام بود دارید.
اگر هدف رسم دیاگرام بود از اغتشاش به خروجی باشه باید اول تابع تبدیل از ورودی اغتشاش به خروجی محاسبه بشه
محمدرضا
با سلام و خسته نباشید
میشه رفرنس های روش lmi رو هم بگین که بتونم رفرنس دهی بکنم .ممنون میشم
alij63@gmail.com
سلام
اولا که LMI روش نیست و صرفا یک ابزاره
ثانیا رفرنس خاصی وجود نداره و از مقالاتی که استفاده کردید، بهشون ارجاع بدید
هادی
با عرض سلام و خسته نباشید.
اگر روش های مطرح شده به طور مشابه برای سیستم های خطی به همراه ترم غیرخطی جداگانه به کار رود، باز هم از کلمه “H inf” می توان استفاده کرد یا خیر؟
به این دلیل برایم سوال شده است که برای سیستم های غیرخطی، تابع تبدیل وجود ندارد تا نرم H inf آن گرفته شود.
ممنون می شوم راهنمایی بفرمایید.
متشکرم
alij63@gmail.com
برای سیستمهای غیرخطی از عبارت L2-gain stability استفاده میشه.
سرچ کنید کلی منبع در موردش هست