در بسیاری از سیستمهای کنترل سیگنالهای مزاحمی به نام اغتشاش وجود دارند که عملکرد حلقه بسته را تحت تاثیر قرار میدهند و عموما ما اطلاع چندانی از ماهیت آنها نداریم. تنها چیزی که از آنها میدانیم این است که دارای انرژی محدود هستند و بینهایت نیستند. یکی از روشهای پرکاربرد و مفید برای تضعیف این اغتشاشات کنترل مقاوم ∞H است. متاسفانه برای حل مساله تضعیف اغتشاش با استفاده از روش ∞H (با دستورات آماده متلب) باید سیستم حلقه باز را به شکل استاندارد موجود در تئوری ∞H دربیاورید تا بتوانید از تولباکس آماده متلب استفاده کنید. این کار مستلزم مطالعه پیشنیازهای فراوان ریاضی و مطالعه کل تئوری ∞H است. خوشبختانه راههای سادهتری برای این مساله وجود دارد. در این سری جلسات مساله تضعیف اغتشاش را با استفاده از نامساوی های ماتریسی خطی یا LMI خدمت شما تقدیم میکنم. کل مبحث طی چهار جلسه خلاصه شده و LMI های مورد نیاز برای محاسبه بهره کنترل کننده فیدبک حالت بدست آمده است. کسانی که به اثبات قضیه علاقمند نباشند کافی است که ماتریسهای سیستم مورد نظرشان را داخل کد ارائه شده قرار بدهند و بهره کنترل کننده فیدبک حالت مقاوم را بدست آورند. کسانی هم که دوست دارند بیشتر عمیق بشوند، میتوانند اثبات کامل پایداری را به روش مستقیم لیاپونوف که در جلسه دوم ارائه شده، ملاحظه کنند. با امید به اینکه مورد رضایت شما عزیزان قرار بگیرد…
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
معرفی مفاهیم پایه Passivity، Dissipativity و L2-gain Stability و ارتباط با روش ∞H
در این جلسه ابتدا برخی توضیحات کلی در مورد کنترل مقاوم ارایه شده و روشهای متفاوت موجود در این حوزه معرفی میشوند. همچنین مزایای استفاده از نامساویهای ماتریسی خطی برای حل مساله کنترل مقاوم نسبت به روشهای مرسوم مانند ∞H بیان میشود. در ادامه تعریف سیستمهای تلف کننده (dissipative) و دو زیر مجموعه مهم آن یعنی سیستمهای پسیو (passive) و پایدار بهره ال2 (L2-gain stable) بحث شده و رابطه بین این مفاهیم پایداری بیان میشود. در انتها ارتباط انواع پایداری در حالت خاص سیستمهای خطی با نرم ∞H سیستم مطرح شده و مفهوم تضعیف اغتشاش با این نرم بر اساس کتاب غیرخطی خلیل تشریح میشود.
مدت زمان آموزش: 70 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و کتاب کنترل غیرخطی خلیل
پیش نمایش جلسه اول:
جلسه دوم:
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
در این جلسه با توجه به مقدمات ذکر شده در جلسه قبل و با استفاده از تئوری پایداری لیاپونوف شرط نامساوی ماتریسی خطی برای تضمین تضعیف اغتشاش محاسبه میگردد. برای این کار برخی از ترفندهای LMI مانند تبدیل متجانس (congruent transformation) و schur complement مورد استفاده قرار میگیرد. همچنین نحوه فراهم سازی پارامترهای آزاد و بهره L2 سیستم برای حل LMI تشریح میشود.
مدت زمان آموزش: 68 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و مقاله مورد اشاره در فیلم
پیش نمایش جلسه دوم:
جلسه سوم:
پیادهسازی کنترلکننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیهسازی در متلب
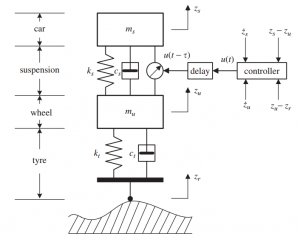
در این جلسه روش تضعیف اغتشاش بدست آمده در جلسه قبل بر روی یک مدل یک چهارم سیستم تعلیق فعال خودرو پیاده شده است. لازم به ذکر است که تمامی LMI ها با استفاده از تولباکس YALMIP در محیط متلب حل شده اند و بنابراین شما باید این تولباکس را قبل از اجرای کدها بر روی متلب نصب کرده باشید. برای توضیحات تکمیلی درباره نحوه دانلود و نصب تولباکس YALMIP به جلسه ششم از سری فیلمهای آموزش حل ناتساویهای ماتریسی خطی مراجعه فرمایید. همچنین نحوه تعیین خروجی رگوله شده (penalty vector) برای سیستم تعلیق و ماتریسهای آزاد برای طراحی کنترل کننده مقاوم تشریح شده است. بعد از طراحی کنترل کننده فیدبک حالت، سیستم حلقه بسته برای دو حالت فعال و غیر فعال شبیه سازی شده و نتایج باهم مقایسه شده اند. نتایج شبیهسازی نشاندهنده عملکرد مطلوب کنترل کننده مقاوم در برابر انواع مختلف پروفایل جاده نسبت به کنترل غیر فعال است.
مدت زمان آموزش: 71 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس – کدهای متلب مربوط به طراحی و شبیهسازی و مقاله مورد استفاده در طراحی و شبیهسازی
پیش نمایش جلسه سوم:
جلسه چهارم:
حل مساله ردیابی برای سیستمهای دارای اغتشاش خارجی
در این جلسه ابتدا قانون کلی ردیابی برای سیستمهای خطی و به خصوص برای سیستم خطی دارای اغتشاش خارجی استخراج شده و ساختار کنترل کننده مقاوم فیدبک حالت که به طور همزمان قادر به حل مساله تضعیف اغتشاش و ردیابی است؛ معرفی میشود. در ادامه روش فوق برای سیستم تعلیق فعال که در جلسه پیش مساله رگولاسیون برای آن حل شده بود؛ اعمال شده و کنترل کننده مورد نظر بر روی سیستم تعلیق اعمال شده و عملکرد آن مورد ارزیابی قرار میگیرد. همچنین اثر سیگنال مرجع با فرکانس های متفاوت نیز روی حالتهای سیستم طی شبیهسازیهای مختلف بررسی میشود.
مدت زمان آموزش: 66 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و کدهای متلب مربوط به طراحی و شبیهسازی
حجم فایل: 105 مگابایت
پیش نمایش جلسه چهارم:
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم




mohammad
سلام وروز بخیر جناب اقای دکتر ببخشید ی سوال داشتم خدمتتون در مورد ساختار سیستم تعلیق که زحمت شبیه سازی کشیدین ببخشید جناب اقای دکتر در سیستم تعلیق خودرو این MUکه فرمودین جرم چرخ هستش و با ی فنر و دمپر به جرم ماشین MS وصله چرا در پایین دوباره فنر داریم و ببخشید ی سوال دیگه جناب اقای دکتر
منظورتون ازZU-ZR چیه و در شکل نمایش سخت افزار ببخشید اون جرم کوچک که دایره ای هست و سیاه تو چر است وروی زمین قرار داره چیه و چه فرقی با چرخ که با MU مدل کردیم داره ممنون میشم راهنماییم کنید با تشکر
علی جوادی
سلام
فنر پایینی نشون دهنده مدل تایر هست
zu-zr همون تغییرات ارتفاع تایر هست
اون نقطه سیاه محل اتصال تایر با زمینه
از اونجایی که مدل ODE هست بنابراین مدل تایر چگال فرض شده
برای اطلاعات بیشتر در مورد سیستم تعلیق به آموزش زیر مراجعه کنید:
https://www.controlref.com/suspension/
محمد
با سلام و روز بخیر جناب اقای دکتر ببخشید در جلسه 3 انتهای جلسه که در مورد اغتشاش raf road صحبت می کردین گفتین 4 جلسه جداگانه در مورد سیستم تعلیق صحبت کردین ممنون میشم لینک و یا نام جلسات بدید تا بتونم ببینمشون با تشکر
علی جوادی
سلام
به لینک زیر مراجعه کنید:
https://www.controlref.com/suspension/
امید
با سلام و عرض ادب خدمت استاد محترم دکتر جوادی:
من lmi های موجود در آموزشتون رو در تولباکس یالمیپ ران میکنم infeasible میشه.حتی بردمش تو تولباکس cvx باز هم infeasible شد.لطفا راهنمایی کنید
سپاس
علی جوادی
اقدام شد
احسان
با عرض سلام و خسته نباشید خدمت شما استاد محترم.
در درس کنترل خطی، برای اینکه خروجی سیستم، سیگنال پله را دنبال کند، خطای بین سیگنال پله و خروجی سیستم را به کنترل کننده اعمال می کردیم.
در آنجا ur را به خروجی کنترل کننده اضافه نمی کردیم.
چرا در آنجا بدون اینکه ur را بدهیم، انتظار داشتیم سیگنال پله دنبال شود؟
در واقع چه تفاوتی بین این دو وجود دارد؟
با تشکر از زحمات گرانقدر شما استاد محترم
علی جوادی
سلام
اگر نقطه تعادل مبدا باشه ur برابر صفره. احتمالا در درس کنترل خطی نقطه تعادل مبدا بوده
پری
سلام من میخوام این فیلم رو تهیه کنم اما قبلش میخوام مطمئن شم برای سیستمی که دارم (یک مقاله) به کار میاد یا خیر. خواهش میکنم زود پاسخ بدید. اگه ممکنه به ایمیلم پیام بدین که مقاله رو بفرستم ببینید. مرسی
علی جوادی
@پری,
اقدام شد
نعیم
سلام و عرض خسته نباشید
می خواستم ببینم چه زمانی کنترل مقاوم ∞H سیستمهای غیر خطی تحت اغتشاش با استفاده از نامساویهای ماتریسی خطی (LMI) رو بیان میکنید؟
علی جوادی
@نعیم,
سلام
برای سیستمهای غیرخطی در حالت کلی روش کنترل مقاوم ارائه نشده ولی برای دسته ای از سیستمهای غیرخطی روشهایی وجود داره. البته بعضی از روشها هم هستند که کلیتر هستند ولی حل معادلات نهایی بدست اومده سخته به خاطر اینکه به نامساوی ماتریسی منجر نمی شوند. امیدوارم در آینده فرصت بشه در مورد روشهای مختلف صحبت کنم.
منصور
سلام من میخوام این فیلم رو تهیه کنم اما قبلش میخوام مطمئن شم برای سیستمی که دارم (یک مقاله) به کار میاد یا خیر. خواهش میکنم زود پاسخ بدید. اگه ممکنه به ایمیلم پیام بدین که مقاله رو بفرستم ببینید. ممنون از لطفتان
علی جوادی
@منصور,
سلام
اقدام شد
شهرام
سلام من میخوام این فیلم رو تهیه کنم اما قبلش میخوام مطمئن شم برای سیستمی که دارم (یک مقاله) به کار میاد یا خیر. خواهش میکنم زود پاسخ بدید. اگه ممکنه به ایمیلم پیام بدین که مقاله رو بفرستم ببینید. مرسی
علی جوادی
@شهرام,
سلام. اقدام شد
رضا
سلام جناب آقای دکتر جوادی
یه سوال داشتم از خدمتتون
سیستم های غیر خطی رو ابتدا خطی سازی میکنیم و سپس کنترل کننده مقاوم رو به گونه ایی طراحی میکنیم که در حوالی نقطه کار اثر اغتشاش رو روی خروجی کم کنند
حالا اگر بخواهیم عملکرد کنترل کننده طراحی شده رو روی سیستم غیر خطی بررسی کنیم آیا روش اویلر که بکار بردید باز هم معتبره ؟
یعنی بصورت X_i+1 = X_i + f(x,u,w,t)*delta
علی جوادی
@رضا,
سلام
بله باز هم معتبره. البته تا حد ممکن باید dt کوچیک انتخاب بشه
رامین
باسلام..فیلمهای پیش نمایش باز نمیشه
مدیر سایتادمین سایت
@رامین,
سلام
توی اینترنت اکسپلورر امتحان کنید. اگه باز نشد احتمالا فلش پلیر روی سیستمتون نصب نیست باید اونو نصب کنید
درود