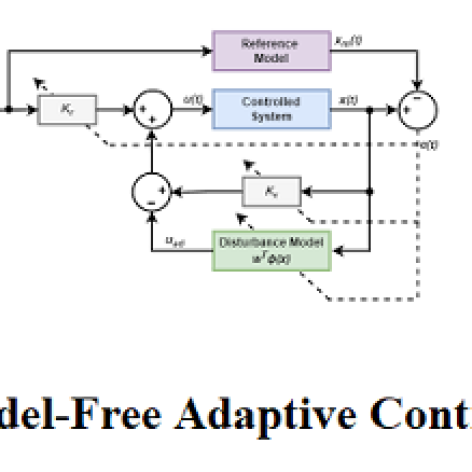
کنترل تطبیقی مستقل از مدل(Model-Free Adaptive Control) یکی از روشهای نوین و مؤثر در حوزه کنترل دادهمحور (Data-Driven Control) است که بدون نیاز به مدلسازی دقیق سیستم، امکان طراحی کنترلکنندههای پایدار و عملکرد محور را فراهم میکند. این روش که بر پایه خطیسازی دینامیک به فرم فشرده
(Compact Form Dynamic Linearization) یا (CFDL)
بنا شده، دیدگاه جدیدی در طراحی کنترل برای سیستمهای غیرخطی، دارای تأخیر، و نامعین ارائه میدهد.
در این روش، برخلاف روشهای کلاسیک که نیازمند شناخت مدل دقیق دینامیکی هستند، تنها با استفاده از دادههای ورودی و خروجی سیستم، کنترلکننده طراحی میشود. این ویژگی باعث میشود که کنترل بدون مدل، گزینهای مناسب برای سیستمهایی با مدلهای پیچیده یا ناشناخته باشد.
مرجع
Zhijun Li, Jun Luo, Model-Free Adaptive Control: Theory and Applications, CRC Press, 2017
یکی از منابع مهم در زمینه کنترل بدون مدل است که مباحث نظری و کاربردی را با زبانی منسجم و ساختاریافته ارائه میدهد. در این آموزش، تلاش میشود تا مفاهیم بنیادی این روش به زبانی ساده و کاربردی برای سیستم های غیرخطی چندورودی-چندخروجی (MIMO) و تک ورودی-تک خروجی (SISO)آموزش داده شود و سپس با استفاده از مثالهای عددی و کاربردی، درک بهتری از نحوه پیادهسازی کنترلکنندههای تطبیقی بدون مدل حاصل شود.
در این آموزش، شما خواهید آموخت:
- مفهوم خطیسازی دینامیک به فرم فشرده (CFDL) و نقش آن در طراحی کنترل بدون مدل
- نحوه طراحی الگوریتمهای MFAC برای سیستمهای تکورودی-تکخروجی (SISO) و چندورودی-چندخروجی (MIMO)
- تحلیل همگرایی و پایداری کنترلکنندههای طراحیشده بدون نیاز به مدل
- نحوه پیادهسازی عملی MFAC در محیط متلب (MATLAB) با استفاده از مثال های متنوع
جلسه اول: معرفی کنترل تطبیقی مستقل از مدل برای سیستم های غیرخطی تک ورودی-تک حروجی
در کنترل کلاسیک، طراحی کنترلکنندهها معمولاً نیازمند مدل دقیق ریاضی از سیستم است، اما در بسیاری از کاربردهای واقعی، دسترسی به چنین مدلی دشوار یا غیرممکن است. کنترل تطبیقی مستقل از مدل (Model-Free Adaptive Control) روشی نوین در مهندسی کنترل است که بدون نیاز به مدل دینامیکی سیستم، تنها با استفاده از دادههای ورودی و خروجی، یک کنترلکننده تطبیقی طراحی میکند. این رویکرد بر پایه مفهوم خطیسازی دینامیکی به فرم فشرده (CFDL) بنا شده و امکان کنترل سیستمهای غیرخطی، دارای عدم قطعیت، و متغیر در زمان را فراهم میسازد. در این جلسه با مزایا و دلایل رویکرد بدون مدل آشنا میشویم و میبینیم که چگونه MFAC به عنوان یک ابزار قدرتمند دادهمحور، در حال تبدیل شدن به یک گزینه محبوب در کنترل سیستمهای پیچیده است.
جلسه دوم: تخمین تابع متغیر با زمان PPD و طراحی کنترل کننده مستقل از مدل برای سیستم های SISO
در ادامه معرفی کنترل تطبیقی مستقل از مدل، در این جلسه با مفهوم کلیدی تابع دینامیکی شبهجزئی (Pseudo Partial Derivative – PPD) آشنا میشویم که نقش محوری در استخراج مدل خطیشده سیستم بهصورت دادهمحور دارد. این تابع، که یک کمیت متغیر با زمان است، رفتار دینامیکی سیستم را بهصورت تقریبی توصیف میکند و بدون نیاز به دانستن ساختار سیستم، از روی دادههای ورودی و خروجی برآورد میشود. با تخمین لحظهای PPD، میتوان یک قانون کنترل ساده و تطبیقی طراحی کرد که در سیستمهای SISO، باعث ردیابی مطلوب سیگنال مرجع و پایداری بسته میشود. در این جلسه، ضمن بررسی نحوه استخراج PPD، فرآیند طراحی و بهروزرسانی کنترلکننده MFAC را برای سیستمهای تکورودی-تکخروجی بهصورت گامبهگام تشریح میکنیم.
جلسه سوم: اثبات پایداری کنترل مستقل از مدل برای سیستم های غیرخطی SISO
در این جلسه به بررسی پایداری کنترلکننده مستقل از مدل برای سیستمهای غیرخطی SISO میپردازیم. برخلاف روشهای سنتی که معمولاً بر اساس توابع لیاپانوف پایداری را اثبات میکنند، در MFAC از رویکردی دادهمحور استفاده میشود که با تحلیل تفاوتی و کرانگذاری مناسب، نشان میدهد خطای ردیابی در حلقه بسته بهتدریج کاهش یافته و به مقدار کوچکی همگرا میشود. در این روش، با استفاده از تخمین تابع متغیر با زمان PPD و طراحی مناسب بهره کنترل، میتوان اثبات کرد که سیگنالهای ورودی و خروجی سیستم کراندار باقی میمانند و رفتار کلی سیستم پایدار خواهد بود. در این جلسه گامبهگام روند این اثبات را دنبال میکنیم و شرایطی را که تضمینکننده پایداری و همگرایی در MFAC هستند، مورد بررسی قرار میدهیم.
جلسه چهارم: ادامه بحث پایداری و شبیه سازی کنترل مستقل از مدل برای سیستم های غیرخطی SISO
در این جلسه، ادامهی بحث پایداری سیستمهای کنترلشده با MFAC را دنبال میکنیم و نتایج نظری ارائهشده در جلسه قبل را با شبیهسازی عددی بررسی خواهیم کرد. هدف این است که نشان دهیم چگونه کنترلکننده مستقل از مدل در عمل میتواند باعث همگرایی خطای ردیابی، حفظ کرانداری سیگنالها، و بهبود عملکرد دینامیکی سیستم شود. با استفاده از یک یا چند سیستم غیرخطی SISO، ابتدا فرآیند تخمین تابع PPD و بهروزرسانی قانون کنترل را پیادهسازی میکنیم و سپس رفتار سیستم در مواجهه با تغییرات مدل و شرایط اولیه مختلف تحلیل میشود. این شبیهسازیها به درک بهتر پایداری و عملکرد MFAC کمک میکنند و نشان میدهند که این روش تا چه حد برای کنترل سیستمهای ناشناخته و پیچیده مؤثر است.
جلسه پنجم: معرفی کنترل تطبیقی مستقل از مدل برای سیستم های MIMO
در این جلسه، رویکرد کنترل تطبیقی مستقل از مدل را به حوزه سیستمهای چند ورودی-چند خروجی (MIMO) گسترش میدهیم. برخلاف سیستمهای SISO که فقط یک ورودی و خروجی دارند، سیستمهای MIMO معمولاً دارای دینامیکهای پیچیدهتر و برهمکنش میان متغیرها (interactions) هستند، که طراحی کنترلکننده را دشوارتر میسازد. در MFAC، با تعمیم مفهوم تابع PPD به ماتریسهای دینامیکی، میتوان رفتار سیستم را بهصورت محلی و دادهمحور مدلسازی کرد و قانون کنترلی را برای تمام ورودیها بهگونهای تنظیم کرد که خروجیها به مراجع خود همگرا شوند. در این جلسه، ساختار کلی MFAC برای سیستمهای MIMO، نحوه تخمین ماتریس PJM و بهروزرسانی پارامترهای کنترلی را معرفی میکنیم و تفاوتهای کلیدی آن با حالت SISO را مورد بحث قرار میدهیم.
جلسه های ششم و هفتم: تحلیل پایداری کنترل تطبیقی مستقل از مدل برای سیستم های MIMO
در این جلسه به تحلیل پایداری سیستمهای چند ورودی-چند خروجی (MIMO) تحت کنترل تطبیقی مستقل از مدل (MFAC) میپردازیم. در این چارچوب، بهجای استفاده از مشتقات دقیق مدل، از ماتریس جاکوبی شبهای (PJM) بهره میگیریم که بهصورت برخط از دادههای ورودی و خروجی تخمین زده میشود. با استفاده از این ماتریس و طراحی یک قانون کنترلی مناسب، نشان داده میشود که خطای ردیابی تمام خروجیها به ناحیهای کوچک همگرا میشود و سیگنالهای سیستم در حلقه بسته کراندار باقی میمانند. تحلیل پایداری در این سیستمها با استفاده از روابط برداری و تکنیکهای ماتریسی انجام میشود که تعمیمیافته نسخه SISO است، اما تعاملات بین کانالها را نیز در نظر میگیرد. این جلسه پایهای نظری برای اطمینان از عملکرد MFAC در سیستمهای پیچیدهتر فراهم میسازد.
جلسه هشتم: ادامه تحلیل پایداری کنترل تطبیقی مستقل از مدل و شبیه سازی آن برای سیستم های MIMO
در این جلسه، ادامه تحلیل پایداری سیستمهای چند ورودی-چند خروجی (MIMO) تحت کنترل تطبیقی مستقل از مدل (MFAC) را دنبال میکنیم و نتایج نظری که در جلسات قبل مطرح شد را با استفاده از شبیهسازیهای عددی بررسی خواهیم کرد. پس از اینکه اثبات پایداری در سیستمهای MIMO با استفاده از تخمین ماتریس جاکوبی شبهای (PJM) ارائه شد، در این جلسه نشان میدهیم که چگونه میتوان این تحلیلها را در عمل پیادهسازی کرد. با شبیهسازی سیستمهای MIMO ، تأثیر پارامترهای کنترلی و تخمینهای دادهمحور را بر پایداری و عملکرد سیستم مشاهده میکنیم.
جلسه های نهم و دهم: کنترل تطبیقی مستقل از مدل بهبود داده شده برای سیستم های غیرخطی SISO
در این جلسه، به بررسی نسخه بهبود یافته کنترل تطبیقی مستقل از مدل (MFAC) برای سیستمهای غیرخطی تک ورودی-تک خروجی (SISO) میپردازیم. این رویکرد بهخصوص برای بهبود عملکرد و پایداری در سیستمهای غیرخطی که دارای تغییرات زیاد در پارامترها، نویز بالا و عدم قطعیتهای بزرگ هستند، طراحی شده است. با بهکارگیری الگوریتمهای پیشرفته برای تخمین دقیقتر ماتریس جاکوبی شبهای (PJM) و تنظیم دینامیکی پارامترهای کنترلکننده، میتوان عملکرد سیستم را در شرایط پیچیدهتر بهبود بخشید. در این رویکرد، ضرایب به صورت آنلاین از طریق حل معادلات LMI (Linear Matrix Inequalities) بهروزرسانی میشوند، که این امکان را میدهد تا سیستم بهطور دایم به شرایط تغییر یافته پاسخ دهد. این تغییرات باعث میشود که کنترلکننده نه تنها به ردیابی دقیقتر مرجع برسد، بلکه پایداری سیستم در مواجهه با دینامیکهای پیچیده غیرخطی نیز تضمین شود. در این جلسه، به بررسی نحوه پیادهسازی این بهبودها در شبیهسازیها پرداخته و عملکرد آن را در مقایسه با نسخههای قبلی تحلیل خواهیم کرد.
جلسه های یازدهم و دوازدهم: کنترل تطبیقی مستقل از مدل بهبود داده شده برای سیستم های غیرخطی MIMO
در این جلسات، به بررسی نسخه بهبود یافته کنترل تطبیقی مستقل از مدل (MFAC) برای سیستمهای غیرخطی چند ورودی-چند خروجی (MIMO) میپردازیم. برخلاف سیستمهای SISO، سیستمهای MIMO دارای برهمکنشهای پیچیدهتری میان ورودیها و خروجیها هستند که طراحی و پیادهسازی کنترلکننده را دشوارتر میکند. در این رویکرد بهبود یافته، هدف اصلی بهبود عملکرد و پایداری در سیستمهای MIMO است که در آنها دینامیکهای غیرخطی و عدم قطعیتهای زیادی وجود دارد. با استفاده از الگوریتمهای پیشرفته برای تخمین دقیقتر ماتریس جاکوبی شبهای (PJM) و حل آنلاین ضرایب از طریق LMI، قادر خواهیم بود کنترلکنندههایی طراحی کنیم که بهطور پویا و در لحظه به تغییرات سیستم پاسخ دهند. این رویکرد بهویژه برای سیستمهای پیچیدهتر MIMO که شامل تغییرات گسترده در پارامترها و نویز زیاد هستند، کارآمد است.
جلسه سیزدهم: کنترل تطبیقی مستقل از مدل بهبود داده شده برای سیستم های غیرخطی MIMO
دراین آموزش، شبیهسازی کنترل تطبیقی مستقل از مدل بهبودیافته برای سیستمهای غیرخطی SISO و MIMOبهطور کامل بررسی میشود. این روش بدون نیاز به مدل دقیق سیستم، با تکیه بر دادههای ورودی و خروجی، پارامترهای کنترلکننده را بهصورت بلادرنگ تنظیم میکند تا عملکردسیستم در برابر تغییرات و اغتشاشها حفظ شود. برای پیادهسازی، از محیط MATLAB استفاده میشود و در بخش بهینهسازی، از ابزارهای YALMIPو CVX برای حل مسائل LMI، و همچنین از تابع fminconبرای حل مسائل بهینهسازی غیرخطی استفاده خواهد شد. این ترکیب به طراح اجازه میدهد تا کنترلکنندهای با کارایی بالا، حتی در حضور محدودیتهای فیزیکی یا قیدهایغیرخطی، پیادهسازی کند. در پایان، با تحلیل پاسخ سیستم به ورودیهای مختلف، تأثیر نویز، و ارزیابی معیارهای عملکرد، پایداری و دقت کنترلکننده مورد بررسی قرار میگیرد.
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



دیدگاهها
هیچ دیدگاهی برای این محصول نوشته نشده است.