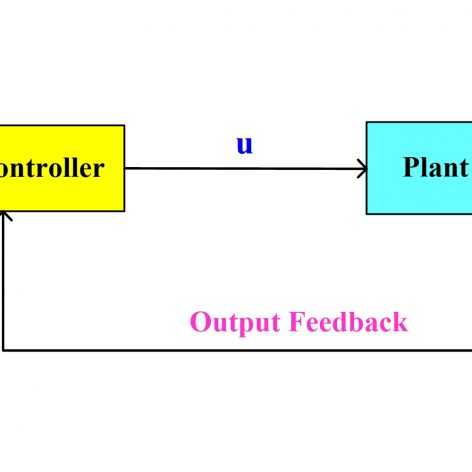
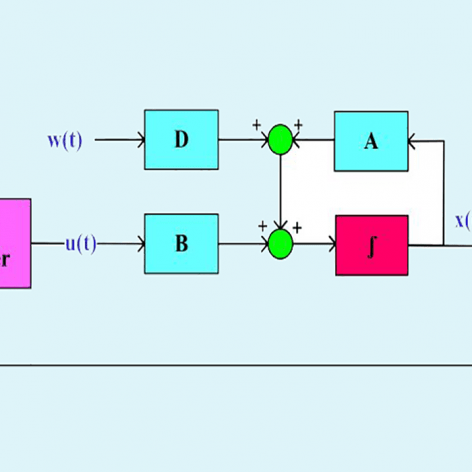
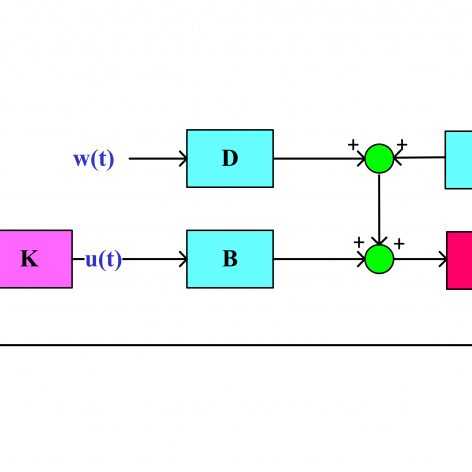
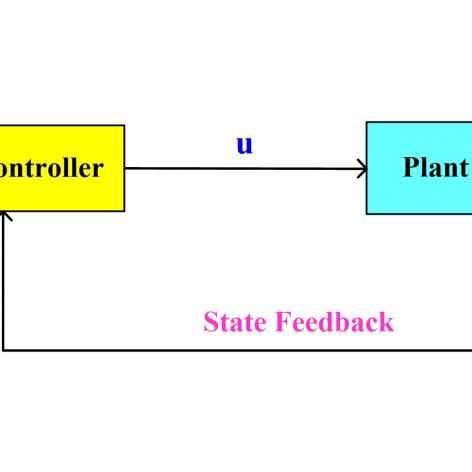
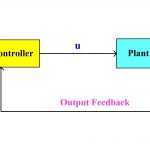
در آموزشهای قبلی، کنترل فیدبک حالت بهینه LQR مورد بررسی قرار گرفت که فرض اساسی آن در دسترس بودن تمام حالتهاست. با توجه به محدود کننده بودن این فرض، در آموزش حاضر، کنترل فیدبک خروجی بهینه (LQG (Linear Quadratic Gaussian معرفی میشود که محدودیت LQR را نداشته و اندازهگیری همه حالتها مورد نیاز نیست. در واقع LQG از یک کنترلکننده بهینه LQR و یک فیلتر کالمن تشکیل شده است که فیلتر کالمن از خروجیهای سیستم تخمین حالتها را در هر لحظه محاسبه کرده و در اختیار کنترلکننده LQR قرار میدهد. مشابه LQR، LQG هم تنها برای سیستمهای خطی بهینه است اما میتوان با استفاده از خطیسازی ژاکوپی برای سیستمهای غیرخطی نیز از آن استفاده کرد. در این مجموعه آموزشی نحوه طراحی و پیادهسازی کنترلکننده LQG برای سیستمهای خطی و غیرخطی در محیط نرمافزار متلب آموزش داده میشود.
پیشنیاز: آشنایی اولیه با نرم افزار متلب – تئوری سیستمهای خطی – کنترل فیدبک حالت بهینه LQR
جلسه اول:
معرفی کنترل فیدبک خروجی بهینه LQG
جلسه دوم:
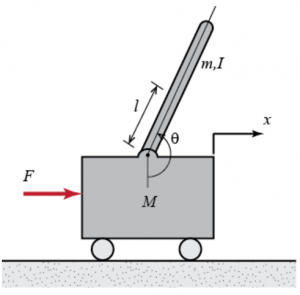
طراحی رگولاتور LQG و یک سروو کنترلر انتگرالی LQG برای سیستم پاندول معکوس و شبیهسازی در متلب
جلسه سوم:
طراحی و شبیهسازی رگولاتور هیبریدی LQG و یک سروو کنترلر هیبریدی LQG برای سیستم پاندول معکوس
جلسه چهارم:
طراحی کنترلکننده بهینه LQG برای سیستمهای غیرخطی و پیادهسازی بر روی سیستم شناور مغناطیسی
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم




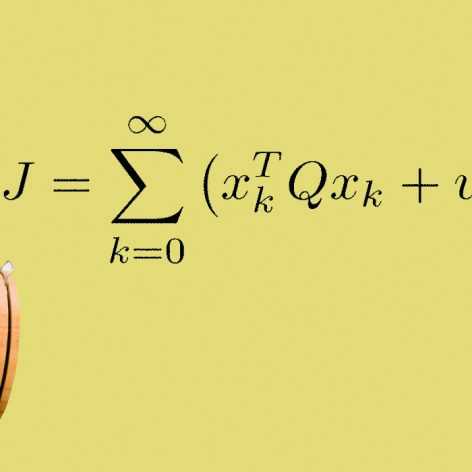

محمد عبداله زاده
سلام دوباره خدمت شما اقای دکتر ببخشیدکنترل فازی و یامد لغزشی بر روی شناور مغناطیسی پیاده سازی نکردین؟
علی جوادی
@محمد عبداله زاده,
خیر. فازی و مدلغزشی در تخصص من نیست
محمد عبداله زاده
با سلام خدمت شما اقای دکتر ببخشید تو فیلم گفتین شناور مغناطیسی قبلا بحث کردین میتونم بپرسم غیر از lqrو lqg چه کنترل کننده ای برای شناور مغناطیسی طراحی کردیم من بتونم اموزشاتون تهیه کنم
علی جوادی
@محمد عبداله زاده,
سلام
جلسات 10 و 11 سری فیلمهای حل نامساوی ماتریسی خطی در متلب رو ببینید:
https://www.controlref.com/lmi-film/
leo
در این آموزش شما ابتدا کالمن و k بهینه را پیدا می کنید و سپس اون رو در داخل سیمولینک قرار می دید ولی من می خوام تمام موارد گفته شده در داخل سیمولینک اجرا شود چون ماتریس ضرایب مانند A B C D دائما در حال تغییر هستند مقدار کوواریانس اغتشاش نیز نامعلوم و با اندازه گیری های داخل سیمولینک به دست می آید . حال سوال من اینه که می شه فضای حالت رو که ماتریس های اون در حال تغییر هستند همچنین بهره k رو در داخل سیمولینک انجام داد؟
علی جوادی
@leo,
سلام
داخل سیمولینک بلوکی برای طراحی بهره های کالمن و کنترل کننده وجود نداره و مستقیما نمیشه این کار رو کرد ولی شاید بشه به صورت غیر مستقیم عمل کرد. یعنی از بلوک Interpreted MATLAB Function استفاده کرده و داخلش دستورات مورد نیاز مثل lqr و kalman رو فراخوانی کنید.
البته دقت کنید که تضمینی وجود نداره که برای پارامترهای متغیر با زمان دستورات lqr و kalman بتونند مساله رو (در هر گام زمانی) حل کنند ولی میتونید امتحان کنید
حسین
با سلام و خسته نباشید خدمت دوستان،
من دانشجوی دکتری کشاورزی هستم. برای پایان نامه م نیاز دارم که از فیلتر کالمن استفاده کنم.
خلاصه کار من به اینصورت هست که: مدل شبیه سازی رشد گیاه رو ران میکنیم، همزمان از داده های ماهواره ای هم استفاده میکنیم، هر زمانی که داده ماهواره ای وجود داشته باشه، باید متغیر شبیه سازی شده در مدل، بر اساس داده ماهواره ای آپدیت بشه. مقالاتی که من خودندم، همگی فیلتر کالمن رو پیشنهاد کردند.
ممنون میشم که کمکم کنید که از کجا باید شروع کنم.
با تشکر
حسین
علی جوادی
@حسین,
سلام
برای شروع به کار با کالمن به صفحه تخمین بهینه حالت مراجعه کنید و در قدم اول راهنمای استفاده از جلسات رو حتما ببینید. اگر باز سوالی داشتید داخل همون صفحه مطرح کنید
امیر
سلام
در شبیه سازی یه مقاله که میشه گفت در حوزه کنترل مقاوم هست به مشکل خوردم، البته مثال مقاله رو شبیه سازی کردم اما وقتی پارامترهای سیستم رو تغییر میدم و کنترلر رو باز طراحی میکنم خروجی سیستم ناپایدار میشه. از لحاظ تئوری سیستم باید پایدار باشه اما در عمل این اتفاق نمی افته. خواستم ببینم شبیه سازی هم انجام میدین؟ البته فایل هاش آمادس و زیاد وقتتون رو نمیگیره؟
با تشکر
علی جوادی
@امیر,
سلام
الان درگیر پیش دفاع هستم و اصلا فرصت ندارم. عذرخواهی منو بپذیرید
رضا
سلام آقای جوادی
ممنون از موضوع خوبی که انتخاب کردید.
robust optimal control هم جز آموزشتون هست ؟
چون آموزش های مقاوم رو هم خودتون روی سایت قرار دادید
علی جوادی
@رضا,
با سلام و تشکر از لطف شما
اگر مشکل خاصی پیش نیاد، بعد از تاخیر (که در حال آماده سازیش هستم)، نوبت ∞H2/H هستش که هم مقاومه و هم بهینه