کنترل مقاوم به دلیل کاربردهای خیلی زیاد یکی از حوزه های مهم در تئوری کنترل محسوب میشود. عموما وقتی صحبت از کنترل مقاوم میشود همه به یاد ∞H و LFT و کلی ریاضیات پیچیده مثل تعریف نرم ها و فضاهای علمی تخیلی دیگر (مثل فضای هاردی) میافتند. وقتی بنده درس سه واحدی کنترل مقاوم را گذراندم، احساس کردم برای این کار باید راههای راحت تر و بهتری وجود داشته باشد! تا اینکه با LMI آشنا شدم و دیدم که چطور بعضی ها توانستهاند هر مساله کنترلی را به نامساوی ماتریسی خطی تبدیل کنند، از جمله حذف نامعینی و تضعیف اغتشاش. اگر نگاهی به مقالات 10-15 سال اخیر در زمینه کنترل بیندازید، خواهید دید که در اکثر موارد (کنترل مقاوم یا غیر مقاوم) از روش مستقیم لیاپونوف استفاده کرده و مساله پایداری را به LMI تبدیل میکنند. برای اینکه این تجربه را به شما هم انتقال بدهم، تصمیم گرفتم که روشهای بر مبنای LMI را برای مسایل مختلف کنترلی از قبیل حذف نامعینی؛ تضعیف اغتشاش؛ طراحی رویتگر و … به تدریج در سایت قرار بدهم. برای شروع، در این سری جلسات نحوه فرمولبندی مساله حذف نامعینی پارامتری را برای سیستمهای خطی به صورت LMI تقدیم میکنم. با امید به اینکه برای شما مفید واقع بشود.
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
معرفی مقدماتی کنترلکننده های مقاوم و انواع نامعینی ها
در این جلسه ابتدا برخی توضیحات کلی در مورد کنترل مقاوم ارایه شده و روشهای متفاوت موجود در این حوزه معرفی میشوند. همچنین مزایای استفاده از نامساویهای ماتریسی خطی برای حل مساله کنترل مقاوم نسبت به روشهای مرسوم مانند ∞H بیان میشود. در انتها انواع نامعینیها تعریف شده و روشهای مرسوم برای مدلسازی نامعینی بر اساس یک مقاله ISI معرفی میشود.
مدت زمان آموزش: 69 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و مقاله های مورد اشاره در فیلم
حجم فایل: 145 مگابایت
پیش نمایش جلسه اول:
جلسه دوم:
طراحی کنترل کننده مقاوم به دو روش مقدار ویژه و روش مستقیم لیاپونوف برای یک سیستم اسکالر و شبیهسازی در متلب
در این جلسه ابتدا روشهای مختلف پایداری لیاپونوف معرفی شده و به صورت مختصر توضیح داده میشوند. سپس برای یک مثال اسکالر دارای نامعینی به دو روش مقدار ویژه و روش مستقیم لیاپونوف کنترل کننده مقاوم طراحی میشود. در انتها با کنترل کننده بدست آمده سیستم حلقه بسته در محیط متلب شبیهسازی میگردد.
مدت زمان آموزش: 55 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس و کد متلب مربوط به مثال
حجم فایل: 83 مگابایت
پیش نمایش جلسه دوم:
جلسه سوم:
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
در این جلسه سیستمهای خطی با نامعینی پارامتری در حالت کلی در نظر گرفته شده و با استفاده از روش مستقیم لیاپونوف نحوه استخراج نامساوی ماتریسی خطی برای بدست آوردن بهره کنترل کننده فیدبک حالت تشریح میشود. سپس برای مثال اسکالر معرفی شده در جلسه دوم با حل LMI بدست آمده یک کنترل کننده مقاوم طراحی میشود.
مدت زمان آموزش: 77 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس- مقاله مورد اشاره در فیلم و کد متلب مربوط به مثال
حجم فایل: 106 مگابایت
پیش نمایش جلسه سوم:
جلسه چهارم:
مدلسازی نامعینی برای سیستم پاندول معکوس
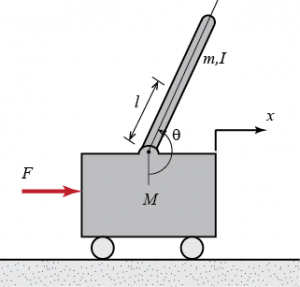
در این جلسه ابتدا دینامیک خطی پاندول معکوس معرفی میشود. با توجه به اهمیت مدلسازی نامعینی جهت طراحی کنترل کننده نحوه مدلسازی نامعینی به شکل استاندارد بیان شده در جلسات قبل برای سیستم پاندول معکوس تشریح میشود. برای سادگی مساله در این جلسه تنها یکی از پارامترهای پاندول معکوس نامعین در نظر گرفته میشود و نحوه مدلسازی این نامعینی روی ماتریسهای سیستم به تفصیل بررسی میشود.
مدت زمان آموزش: 64 دقیقه
محتویات درس: فیلم با کیفیت 720p و پاورپوینت درس
حجم فایل: 100 مگابایت
پیش نمایش جلسه چهارم:
جلسه پنجم:
پیادهسازی کنترلکننده مقاوم بر روی سیستم پاندول معکوس و شبیهسازی در متلب
در این جلسه الگوریتم مرحله به مرحله طراحی کنترل کننده مقاوم برای سیستمهای خطی با نامعینی پارامتری ارائه شده و برای حالتی که یکی از پارامترهای سیستم پاندول معکوس نامعین باشد. مدلسازی نامعینی در محیط متلب انجام شده و نامساوی ماتریسی خطی برای آن حل شده و بهره کنترل کننده فیدبک حالت مقاوم بدست آمده و سیستم حلقه بسته شبیهسازی میشود. در مرحله بعد فرض میشود که دو تا از پارامترهای سیستم پاندول معکوس نامعین بوده و همه مراحل قبل تکرار میشود. در تمامی حالتها عملکرد کنترل کننده فیدبک حالت مقاوم با یک کنترل کننده فیدبک حالت غیر مقاوم مقایسه شده و مقاومت کنترل کننده طراحی شده بررسی میشود. در انتها نحوه مدلسازی تعداد بیشتر پارامترها تشریح شده و دلایل احتمالی عدم حل پذیری نامساویهای ماتریسی خطی برای یک سیستم خاص و راه حلهای ممکن توضیح داده میشود. لازم به ذکر است که تمامی LMI ها با استفاده از تولباکس YALMIP در محیط متلب حل شده اند و بنابراین شما باید این تولباکس را قبل از اجرای کدها بر روی متلب نصب کرده باشید. برای توضیحات تکمیلی درباره نحوه دانلود و نصب تولباکس YALMIP به جلسه ششم از سری فیلمهای آموزش حل ناتساویهای ماتریسی خطی مراجعه فرمایید.
مدت زمان آموزش: 85 دقیقه
محتویات درس: فیلم با کیفیت 720p – پاورپوینت درس و کدهای متلب مربوط به طراحی و شبیهسازی
حجم فایل: 150 مگابایت
پیش نمایش جلسه پنجم:
جلسه ششم:
حل مساله ردیابی برای سیستمهای خطی دارای نامعینی پارامتری و اعمال به سیستم پاندول معکوس
در این جلسه بحث ردیابی سیستمهای خطی دارای نامعینی پارامتری به صورت کامل مورد بررسی قرار میگیرد. ابتدا قانون کلی استحصال ورودی کنترلی جهت ردیابی سیگنال مرجع معرفی شده و سپس با مثالهای متعدد و کاربردی نحوه بدست آوردن ساختار کنترل کننده جهت ردیابی سیستم به صورت گام به گام تشریح میشود. در انتها با همین شیوه کنترل کننده مورد نیاز برای ردیابی در سیستم پاندول معکوس که در جلسه پیش مساله رگولاسیون برای آن حل شد؛ طراحی شده و با شبیهسازی سیستم حلقه بسته در محیط m-file مورد ارزیابی قرار میگیرد.
مدت زمان آموزش: 81 دقیقه
محتویات درس: فیلم با کیفیت 720p – پاورپوینت درس و کدهای متلب مربوط به طراحی و شبیهسازی
حجم فایل: 124 مگابایت
پیش نمایش جلسه ششم:
۹۶۰,۰۰۰ تومان قیمت اصلی: ۹۶۰,۰۰۰ تومان بود.۵۹۷,۶۰۰ تومانقیمت فعلی: ۵۹۷,۶۰۰ تومان.Add to cart
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم





الیاس
با عرض سلام و خسته نباشید خدمت استاد گرامی.
سوالی داشتم از خدمتتون.
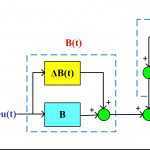
اگر به جای (A(t∆ همانجا کران بالای آن را قرار دهیم و به صورت Ma.F(t).Na ننویسیم، که بعد بخواهیم (F(t را بین یک و منفی یک قرار دهیم و Ma و Na را پیدا کنیم.
آیا مشکلی به وجود می آید؟ به این صورت از محاسبات زیادی راحت می شویم.
با تشکر فراوان
علی جوادی
سلام
اگر این جاگذاری انجام نشه، پس چطور مساله رو به lmi تبدیل کنیم؟
چطور میشه به جای یک مقدار متغیر نامعینی باند بالاش رو قرار بدیم و همچنان معادلات به هم نخوره و در نهایت مساله رو هم به صورت نامساوی ماتریسی در بیاریم؟
پیشنهاد شما چیه؟
الیاس
ببینید من کلا LMI را به این صورت قرار میدهم،
0>[‘(A+∆A)*X+X*(A+∆A)’+(B+∆B)*Y+Y’*(B+∆B)]
و ماتریس های
[B=[0;hB2;0;hB4∆
و
[A=[0 0 0 0;0 hA22 hA23 0;0 0 0 0;0 hA42 hA43 0∆
جایگذاری می کنم.
آیا درست نمی تواند باشد؟
علی جوادی
از کجا معلوم بعد از جاگذاری عبارتی که بدست میاد باند بالای مشتق تابع لیاپونوف باشه؟
شما فقط دارید باند بالای نامعینی رو جاگذاری میکنید در حالیکه باید اثبات کنید عبارتی که بدست میاد باند بالای مشتق تابع لیاپونوف هست تا اینکه برقراری نامساوی بدست اومده، برقراری نامساوی قبلی (قبل از جاگذاری) رو نتیجه بده.
یکم بیشتر فکر کنید
الیاس
با توجه به این که
A(t)< ∆A∆
و
B(t)[‘((A+∆A(t))*X+X*(A+∆A(t))’+(B+∆B(t))*Y+Y’*(B+∆A(t)
0>[‘(A+∆A)*X+X*(A+∆A)’+(B+∆B)*Y+Y’*(B+∆A)]
آیا باند بالای مشتق را نمی توان به این صورت نتیجه گرفت؟
با تشکر از شما
علی جوادی
فرمولها خوانا نیست ولی در هر صورت نمیشه با جاگذاری باند بالای هر جمله، باند بالای کل عبارت رو نتیجه گرفت
امیر یوسف زاده
سلام جناب دکتر جوادی
با تشکر از آموزش های خوبتون
من تمامی آموزش های شما رو که مرتبط با lmi و کنترل مقاوم هستند، خریداری کردم. همراه با آموزش کاربرد متلب در سیستم های کنترل خطی.
موقع دانلود فایل ها، همه فایل ها رو چک نکردم، اما هیچ کدام از ویدئو های آموزش نامساوی های ماتریسی خطی که دقیقا همان موقع مشاهده شون کردم، نیازی به کد نداشتن.
همین طور هیچ کدام از آموزش های طراحی کنترل مقاوم فیدبک خروجی.
اما ویدئو 5 و 6 این اموزش نیاز به کد فعال سازی داره، و همچنین ویدئو 3 و 5 آموزش کنترل فیدبک خروجی از طریق رویتگر با استفاده از LMI.
متاسفانه بنده ایمیل ها رو پاک کردم. از بین 47 ویدئو خریداری شده از وب سایت شما فقط 4 مورد نیاز به کد فعال سازی داره.
چرا مدیر سایت پاسخ گوی چنین مواردی نیستند؟
لطفا تکلیف را مشخص بفرمائید، آیا نیاز به خرید دوباره هست؟
علی جوادی
@امیر یوسف زاده,
سلام
قبلا فایلها هیچکدوم پسورد نداشت ولی به خاطر سو استفاده بعضی سودجوها اخیرا برخی جلسات قفل گذاری شده و دارای پسورد هستن که موقع خرید باید براتون ایمیل شده باشه. البته داخل همون صفحه خرید هم میتونستید پسوردها رو ببینید.
شما به مدیر سایت پیام بدید. من هم بهشون یادآوری میکنم تا پسوردها براتون دوباره ارسال بشه.
نیازی به خرید دوباره هم نیست.
از مشکلاتی براتون پیش اومده عذرخواهی میکنم
امیر یوسف زاده
@علی جوادی, سلام قربان، متشکرم، چند ساعت پیش باهاشون تماس گرفتم، قرار شد چک کنن و برام بفرستن، خیلی ممنونم از پاسخگویی تون.
فرزاد
سلام
من کل جلساتو خریداری کردم و یه سری کده فعال سازی واسم ایمیل کردین
کده فعال سازی جلسه چهارم رو که به صورت آنلاین میزنم میگه اشتباهه به صورت آفلاینم پیام میدم میگه فورمت پیام اشتباهه در صورتی که درستم میفرستم
خواهشا بگید چکار کنم واسه دیدن جلسه چهارم
علی جوادی
@فرزاد,
سلام
بابت این مشکل عذرخواهی میکنم.
من به مدیر سایت انعکاس دادم. امیدوارم هر چه سریعتر مشکل شما حل بشه
فرزاد
سلام، من دیشب کنترل مقاومو خریدم اما هنوز لینک دانلود به ایمیلم فرستاده نشده
علی جوادی
@فرزاد,
سلام
لطفا پوشه اسپم رو چک کنید
نعیم
سلام. فرمت جلسه 4 zxp هستش. چطور بازش کنم؟
علی جوادی
@نعیم,
سلام
از این پلیر استفاده کنید:
https://www.controlref.com/player/
اگر مشکلی بود با مدیر سایت تماس بگیرید
نعیم
@نعیم,
این نرم افزار کد فعال سازی می خواد. میشه لطف کنید بفرستید. من با مدیریت تماس گرفتم ولی جوابگو نبودند
مدیر سایتادمین سایت ( مالک تایید شده )
@نعیم,
من پیگیری میکنم بهتون اطلاع میدم
نعیم
@مدیر سایت,
سلام.مشکلش حل شد.ممنون
مدیر سایتادمین سایت ( مالک تایید شده )
@نعیم,
خواهش میکنم. موفق باشید
محمد
سلام جناب آقای دکترجوادی
اول میخوام ازتون واسه تهیه ی این آموزش های عالی خیلی خیلی تشکرکنم.
جناب آقای دکتر بنده یه سیستم MIMO دارم که 12 ورودی و 4خروجی داره ، می خوام این سیستم رو با روش شناسایی سیستم مدلسازی کنم و عدم قطعیت سیستم رو به روشی که شما فرمودید مدلسازی کنم و راهکار کنترل مقاوم رو روی این سیستم پیاده سازی کنم.
خیلی خیلی ممنون میشم یه راهکاری برای شناسایی این سیستم بهم معرفی کنید که بتونم در نهایت از روشی که شما فرمودید استفاده کنم.
متاسفانه تا الان هرچقدر تلاش کردم موفق به شناسایی نشدم.
خیلی ممنونم
مدیر سایتادمین سایت ( مالک تایید شده )
@محمد,
با سلام و تشکر از لطف شما
در اینجا فرض بر اینه که مدل سیستم معلومه و ماتریسهای سیستم حاوی پارامترهای سیستم هستند. عدم قطعیت در پارامترهای سیستم باعث نامعین شدن ماتریسهای سیستم میشه. اگر ماتریسهای سیستم مستقیما شامل پارامترهای فیزیکی سیستم نباشند، نمیشه فهمید نامعینی چه مفهومی داره و چقدر باید باشه.
بنایراین پیشنهاد من اینه که شما یک ساختار مشخص که ماتریسهای سیستم حاوی پارامترهای سیستم باشند، در نظر بگیرید و سیستم رو طوری شناسایی کنید تا مدل شناسایی شده با داده های واقعی برازش خوبی داشته باشه. بعد باند نامعینی رو پیدا کنید و از روش ارائه شده در اینجا استفاده کنید
پویا
آقای علی جوادی، انقدر این ویدیو ها عالی و فوق العاده هستند که هر روز که یکی از فیلم ها رو نگاه میکنم، دلم میخواد هزاران بار ازتون قدردانی کنم.
واقعا بهترین ها نصیب تون بشه
علی جوادی
@پویا,
باز هم تشکر می کنم
پویا
وای خدای من…. نمیتونم بگم چقدر این مجموعه فوق العاده است…
خدا خیرتون بده…عالیه عالی…
علی جوادی
@پویا,
نظر لطف شماست
رضا
سلام آقای دکتر جوادی
در طراحی هام به یک مشکل برخوردم که تا الان نتونستم راهکار مناسبی رو براش پیدا کنم برای همین مزاحمتون شدم
به دنبال LMI هایی هستم که در فیدبک حالت علاوه بر مدل کردن نامعینی و مقاوم سازی ، قطب های حلقه بسته رو در یک دیسک قرار بده
در کتاب های مختلف برای این کار LMI هایی رو دیدم اما هیچکدوم یک روش سیستماتیک برای مدل کردن عدم قطعیت ارائه نکردن (راستشو بخواید فقط توی ویدید های منحصر بفرد شما یک روش منظم رو دیدم)
متاسفانه به علت کمبود وقتی که برای پایانامم دارم نمیتونم تا آماده شدن این ویدئو درسی از طرف شما صبر کنم. اگر بزرگواری بفرمایید و این LMI ها رو در اختیارم بگذارید ممنون میشم .(هرچند که این لطف شما قابل جبران نیست اما هزینه اون رو هم خدمتتون تقدیم میکنم). قطعا می دونم درگیر ضبط کارهای دیگه هستید اما باور کنید منبع یا فردی که به سبک شما عدم قطعیت رو وارد LMI ها کرده باشه نمی شناسم و کارم متاسفانه یک ماهه که پیش نمیره.
ممنون میشم لطفتون رو از بنده دریغ نفرمایید.
با تشکر
علی جوادی
@رضا,
با سلام
متاسفانه الان سرم خیلی شلوغه و مشغول ریوایز مقاله هام هستم. حتی به صورت خصوصی هم نمیتونم براتون وقت بذارم. بعیده تا تابستون من وقت آزاد داشته باشم.
عذرخواهی منو بپذیرید
رضا
@علی جوادی,
آیا امکانش هست که مقالات یا منبعی که نحوه بدست آوردن این LMI ها رو توضییح داده باشه (با در نظر گرفتن عدم قطعیت پارامتری و به همون صورتی که ویدیو های درسی خودتون هست ) رو بهم معرفی کنید ؟
علی جوادی
@رضا,
در این مورد جست و جو نکردم. زمانی که بخوام جایابی قطب با LMI رو بگم، جست و جو میکنم. اگه بود که از همون مراجع میگم و اگه نبود، مثل قبل سعی میکنم خودم LMI های مربوطه رو بدست بیارم
رضا
سلام آقای دکتر جوادی
دو سوال از خدمتتون داشتم
1- من برای پایانامم یک سیستم دارم که کنترل پذیر و پایداره اما قطب هاش در محل خیلی نامناسبند . به کمک فیدبک حالت معمولی و جایابی قطب های مطلوب، رفتار حالت های سیستم خوب میشه اما وقتی از LMI (حتی بدون در نظر گرفتن نامعینی) استفاده می کنم حالت های سیستم شدیدا ناپایدار میشه. در واقع بردار k که از طریق LMI بدست میاد مناسب نیست . وقتی از LMI استفاده میشه قطب های سیستم در کجا جایابی میشن ؟
متاسفانه در مورد سیستم من با توجه به ناپایدار شدن اونها رو احتمالا به سمت راست برده . برای حل مشکل باید چه کنم ؟ آیا فیدیک خروجی بهم جواب میده؟
2- در جلسه پنجم این مجموعه که برنامه رو توضیح میدید، تا اونجا که من متوجه شدم در LMI مربوط به حالتی که نامعینی نداریم از ماتریس های A , B میانگین استفاده کردید . آیا نباید از A,B که بدون عدم قطعیت استفاده کنیم؟
با تشکر
علی جوادی
@رضا,
با سلام و تشکر از سوال خوبتون
1) اگر سیستم شما پایدار هست دلیلی نداره که یک کنترل کننده پایدارساز (از هر روشی از جمله LMI) براش طراحی کنید. تنها در صورتی این کار توجیه داره که یه عملکرد مدنظر باشه مثلا بخواهید سیستم مقاوم باشه که در اینصورت میتونید کنترل کننده مقاوم طراحی کنید.
با توجه به اینکه جلسه سوم پایداری مجانبی برای سیستم حلقه بسته اثبات شده بنابراین اگر درست طراحی رو انجام بدید و درست داخل متلب شبیهسازی کنید، باید حتما جواب پایدار باشه. البته ممکنه عملکرد زمانی مثل زمان نشست و … مطابق انتظار شما نباشه ولی این موارد جزو تضمینهای روش ارائه شده نیست و باید از روشهای دیگه هم کمک بگیرید. روشهایی وجود دارند که میشه روی قطبهای حلقه بسته شرط گذاشت (از طریق LMI) و به مشخصات زمانی (و یا فرکانسی) دلخواه رسید علاوه بر اینکه سیستم حلقه بسته پایدار بشه. در آینده سعی میکنم این روشها رو هم آموزش بدم.
قطبهای حلقه بسته رو هم به طور تقریبی میتونید از مقادیر ویژه A+BK پیدا کنید ولی چون A و B نامعین هستند، نمیشه دقیقا گفت قطبها کجا هستن. البته اثبات به ما تضمین میده که حتما سمت چپ محور موهومی هستند
2) حق با شماست. بهتر بود من از خود پارامترهای واقعی برای مقایسه استفاده میکردم ولی چون پاسخها خیلی تفاوتی نمیکنه، از ماتریسهای میانگین استفاده کردم
موفق باشید
رضا
@علی جوادی,
با تشکر از پاسخگوییتون ، اگر لطف بفرمایید که بعد از تخمین بهینه بسراغ LMI و کنترل مقاوم برگردید و این مجموعه رو تکمیل کنید بسیار سپاسگزار خواهیم بود.
حق با شماست مجددا از یک سیستم ناپایدار استفاده کردم که مقادیر ویژه اون در نقاط زیره:
1667.73- و 474.73 و 7.5067- و 466.56-
وقتی از دستور place در متلب استفاده میشه قطب ها در محل مطلوب قرار میگیرند و شبیه سازی هم به درستی انجام میشه و حالت ها به سمت صفر میل می کنند
اما وقتی از LMI استفاده میشه مقادیر ویژه سیستم A+BK پایدار میشه و برنامه هم بدرستی نشون میده که LMI بدرستی حل شده اما یکی از قطب ها باز خیلی دوره. مقادیر ویژه سیستم حلقه بسته بصورت زیر میشه:
1653.4- و (31.7j) + (-5.3) و (5.3-) – (31.7j) و 2.04- قرار میگیره ودر شبیه سازی حالت ها به بینهایت میرن
در واقع K که از LMI بدست میاد منجر به این اتفاق میشه ، چون وقتی که K از دستور place بدست میاد همه چی مرتبه و مشکلی نیست در ضمن کل برنامه و شبیه سازی هم در یک فایل نوشته شده و امکان اشتباه وجود نداره چون برای حالتی که K از دستور place بدست میاد همه چی درسته. من برنامه شبیه سازی و خود برنامه LMI رو عینا از کد های خودتون کپی کردم فقط سیستم خودم رو به برنامه دادم
عذرخواهی میکنم که توضییحات بالا کمی زیاد شد اما آیا امکان داره که K مناسب از LMI بدست نیومده باشه و حالت ها به بینهایت برن؟
علی جوادی
@رضا,
اولا که دور بودن قطبها از محور دلیل ناپایداری نیست اتفاقا نشون میده که خیلی هم پایداره و فقط در صورتی میتونه سیستم حلقه بسته ناپایدار بشه که حداقل یکی از قطبها سمت راست محور بیافته.
ثانیا، با توجه به اینکه یکی از قطبها خیلی از محور دوره بنابراین باید موقع حل عددی گام زمانی خیلی کوچک انتخاب بشه. اگر مشکل دیگه ای داخل کد نباشه، من حدس میزنم که اگه گام زمانی 0.001 یا کوچکتر انتخاب بشه (به جای 0.01 که من انتخاب کردم)، احتمال زیاد حل عددی سیستم حلقه بسته همگرا بشه. این کارو بکنید و نتیجه رو همینجا اعلام کنید
اگه مشکل خاصی پیش نیاد، طبق برنامه مباحث مربوط به LMI رو ادامه خواهم داد
رضا
@علی جوادی,
نکته ایی که فرمودید رو اجرا کردم و خوشبختانه جواب گرفتم ، واقعا به موضوعاتی که تدریس میکنید تسلط کامل دارید و بیان بسیار شیوایی در تدریس دارید . سه روزه که برنامه و سیستمم رو بارها چک کردم اما جواب نداد . واقعا ازتون ممنونم
تو نیکی میکن و در دجله انداز که ایزد در بیابانت دهد باز
از اینکه بعد از تخمین بهینه به LMI بر میگردید سپاسگزارم .
جسارتا یک پیشنهاد هم دارم
اگر لطف کنید خودتون و یا یکی از همکاراتون کنترل تطبیقی ، کنترل غیر خطی (در سایتتون بیشتر به طراحی پرداختید) و کنترل مقاوم رو از ابتدا با تئوری کامل و کد نویسی درس بدید به جرات میتونم بگم بهترین سایت کنترل (چه داخلی و چه خارجی) خواهید بود و عملا هیچ دانشجویی به کلاس درسی در دانشگاه نیاز نخواهد داشت ! من درسهای کنترلیمو با اساتیدی مثل پرفسور یزدان پناه و منهاج و جاهد مطلق و …. با نمره های عالی پاس کردم اما مطمئن نیستم به طور عملی چیزهای زیادی یاد گرفته باشم زیرا در کلاس درسی فرصت کافی برای پوشش دادن به همه مطالب(شامل تحلیل و طراحی) وجود ندارد و همچنین هیچ کلاسی هم به تدریس MATLAB نمیپردازد و در نتیجه دانشجو آنچه که باید باشد نیست.
مطالب جدید و مفیدی که در سایت در حال بارگذاری کردنشون هستید گاها با مهندسی کنترل کمی فاصله دارند و پس از مدتی امکان داره سایتتون به سایت های مشابه مثل فرادرس تبدیل بشه و باعث میشه از هدف اولیتون مبنی بر بهترین بودن در کنترل دور بشید.
امیدوارم روز به روز سایتتون پر بار تر بشه (خصوصا از منظر کنترلی)
با تشکر
علی جوادی
@رضا,
خوشحالم که جواب گرفتید.
نظر لطف شماست. در واقع خیلیها هستند که از من تسلط بیشتری دارند اما من این شانس رو پیدا کردم تا در چنین سایتی در خدمت شما باشم.
آموزش کنترل تطبیقی در آینده روی سایت قرار میگیره.
کنترل غیرخطی هم توسط مدیر سایت تکمیل میشه.
در مورد این درسها بهتره پیشنهاداتتون رو به مدیر سایت انعکاس بدید تا اونها رو در آموزشهای آینده در نظر بگیرند.
کنترل مقاوم رو هم خودم ادامه میدم. البته فعلا اولویت با روشهای مقاوم جدیده و روشهای کلاسیک مثل LFT در اولویت دومه. شاید در آینده اون رو هم پوشش بدم.
موفق باشید