کنترل کننده های مقاوم مرتبه کسری

سیستم‌ها و کنترل‌کننده‌های مرتبه کسری (Fractional-Order Systems and Controllers) به عنوان یکی از حوزه‌های نوظهور و پرکاربرد در مهندسی کنترل، افق‌های جدیدی را برای طراحی و تحلیل سیستم‌های دینامیکی گشوده‌اند. این سیستم‌ها با استفاده از ابزارهای ریاضی مبتنی بر حسابان کسری، مفاهیمی فراتر از مدل‌های مرتبه صحیح کلاسیک را به کار می‌گیرند و به‌ویژه در تحلیل سیستم‌های پیچیده و نامعین بسیار مؤثر هستند.

کنترل‌کننده‌های مرتبه کسری، از جمله PID مرتبه کسری (FOPID)، ابزارهای مؤثری برای تنظیم و کنترل سیستم‌ها فراهم می‌کنند. این کنترل‌کننده‌ها با تعمیم اقدامات کنترلی کلاسیک، انعطاف‌پذیری بیشتری برای مقابله با عدم قطعیت‌ها، تأخیرها، و پیچیدگی‌های سیستم‌ها ارائه می‌دهند. با استفاده از این روش‌ها، می‌توان پایداری و عملکرد سیستم‌های پیچیده را به طور قابل‌توجهی بهبود بخشید.

هدف آموزش:

مرجع

Monje, C. A., Chen, Y., Vinagre, B. M., Xue, D., & Feliu-Batlle, V. (2010). Fractional-Order Systems and Controls: Fundamentals and Applications. Springer.

یکی از منابع برجسته در زمینه حسابان کسری و کاربردهای آن در کنترل سیستم‌های دینامیکی است که اصول اساسی و مثال‌های متنوعی از طراحی و تحلیل سیستم‌های مرتبه کسری ارائه می‌دهد. در این آموزش، هدف این است که با زبانی ساده، مفاهیم اولیه حسابان کسری آموزش داده شود و مفاهیم مربوط به پایداری سیستم‌های مرتبه کسری و نحوه طراحی کنترل‌کننده‌های مرتبه کسری به صورت دقیق توضیح داده شود. همچنین، این مفاهیم با ارائه مثال‌های فراوان نشان داده خواهند شد. علاوه بر این، نحوه شبیه‌سازی سیستم‌ها و کنترل‌کننده‌های مرتبه کسری با استفاده از تولباکس FOMCON (Fractional-Order Modeling and Control Toolbox)  در محیط متلب آموزش داده خواهد شد. این بخش به کاربران کمک می‌کند تا دانش تئوری را پیاده‌سازی کنند و ابزارهای لازم برای تحلیل و طراحی سیستم‌های مرتبه کسری را در اختیار داشته باشند. بطور خلاصه آنچه که دراین آموزش یاد خواهید گرفت به صورت زیر است:

• مفاهیم پایه سیستم‌های مرتبه کسری و کنترل‌کننده‌های FOPID توضیح داده می‌شود.
• پایداری و طراحی کنترل‌کننده‌های مرتبه کسری به صورت گام‌به‌گام آموزش داده می‌شود.
• تحلیل پایداری مقاوم و طراحی کنترل‌کننده مرتبه کسری مقاوم برای سیستم‌های نامعین و دارای تأخیر زمانی نیز آموزش داده می‌شود.
• نحوه شبیه‌سازی وشناسایی سیستم های مرتبه کسری با استفاده از FOMCON Toolbox در محیط متلب (MATLAB) ارائه خواهد شد.

جلسه اول: چرا مرتبه کسری؟

 در مهندسی کنترل، مدل‌ها و ابزارهای سنتی معمولاً بر پایه مفاهیم مرتبه صحیح بنا شده‌اند. اما در بسیاری از سیستم‌های واقعی، رفتار دینامیکی پیچیده‌تر از آن است که بتوان با این مدل‌ها به طور دقیق توصیف کرد. حسابان کسری، با استفاده از مشتق و انتگرال مرتبه کسری، این امکان را فراهم می‌کند که رفتار سیستم‌ها با دقت بیشتری مدل‌سازی و تحلیل شود. از سیستم‌های زیستی و الکتریکی گرفته تا فرآیندهای حرارتی و مکانیکی، شواهد زیادی وجود دارد که مدل‌های مرتبه کسری می‌توانند ویژگی‌های واقعی‌تر و کاربردی‌تری نسبت به مدل‌های کلاسیک ارائه دهند. در این جلسه، با مزایای سیستم ها و کنترل کننده های مرتبه کسری و دلایل اهمیت آنها در مهندسی کنترل آشنا خواهیم شد و بررسی می‌کنیم که چرا این رویکرد در حال تبدیل شدن به یکی از ابزارهای اساسی برای طراحی سیستم‌های پیچیده است.

جلسه دوم: انتگرال و مشتق های مرتبه کسری

در حسابان کلاسیک، انتگرال و مشتق همواره به مرتبه‌های صحیح محدود می‌شوند، اما در حسابان کسری این مفهوم گسترش یافته و شامل مرتبه‌های غیرصحیح و حتی کسری می‌شود. انتگرال و مشتق مرتبه کسری، که اساس حسابان کسری را تشکیل می‌دهند، ابزارهایی قدرتمند برای مدل‌سازی رفتارهای پیچیده و حافظه‌دار در سیستم‌های دینامیکی هستند. در این جلسه، ابتدا تعاریف اصلی انتگرال و مشتق مرتبه کسری را معرفی خواهیم کرد و سپس به بررسی روابط ریاضی و مفهوم فیزیکی آن‌ها خواهیم پرداخت. علاوه بر این، نقش توابع ویژه مانند تابع گاما، تابع بتا، و تابع میتگ-لفلر، که به عنوان هسته‌های اصلی در تعریف و کاربرد مشتق و انتگرال‌های مرتبه کسری به کار می‌روند، مورد بحث قرار می‌گیرد. این توابع اهمیت بسیاری در حل معادلات مرتبه کسری و مدل‌سازی دینامیکی دارند. در ادامه، نحوه شبیه‌سازی این توابع در محیط متلب با استفاده از دستورات و ابزارهای مناسب به تفصیل آموزش داده شده است. هدف این است که شرکت‌کنندگان نه‌تنها مفاهیم نظری را درک کنند، بلکه بتوانند این مفاهیم را به صورت عملی پیاده‌سازی کنند و برای کاربردهای واقعی استفاده نمایند.

جلسه سوم: انتگرال و مشتق های مرتبه کسری معادلات دیفرانسیل و سیستم های مرتبه کسری و تحلیل پایداری آنها

در این جلسه، ابتدا نحوه تعریف و حل معادلات دیفرانسیل مرتبه کسری را بررسی خواهیم کرد و سپس سیستم‌های مرتبه کسری را به عنوان مدل‌هایی برای تحلیل دینامیک سیستم‌های مهندسی معرفی می‌کنیم. علاوه بر این، مفاهیم پایداری برای سیستم‌های مرتبه کسری و روش‌های تحلیل آن‌ها از جمله معیارهای پایداری نایکوئیست، و تحلیل طیفی مورد بحث قرار می‌گیرند. در پایان، شبیه‌سازی معادلات و تحلیل پایداری در متلب به‌صورت عملی ارائه  شده است تا شرکت‌کنندگان بتوانند ابزارهای لازم برای مطالعه سیستم‌های مرتبه کسری را در عمل به کار گیرند.

جلسه های چهارم و پنجم: پایداری سیستم های مرتبه کسری

پایداری یکی از مفاهیم اساسی در تحلیل سیستم‌های دینامیکی است که در سیستم‌های مرتبه کسری (Fractional-Order Systems)  به دلیل رفتار پیچیده‌تر و حافظه‌دار بودن این سیستم‌ها، اهمیت بیشتری پیدا می‌کند. در این جلسه، به بررسی روش‌های مختلف تحلیل پایداری سیستم‌های مرتبه کسری خواهیم پرداخت. به طور خاص، از اصل آرگومان (Argument Principle) به عنوان یکی از ابزارهای مؤثر برای تحلیل پایداری این سیستم‌ها استفاده می‌شود. علاوه بر این، سیستم‌های مرتبه کسری به دو دسته همسان  (Commensurate)  و غیرهمسان (Incommensurate) تقسیم می‌شوند، و نحوه استفاده از اصل آرگومان برای هر دو نوع سیستم مورد بحث قرار می‌گیرد. این تحلیل به شرکت‌کنندگان کمک می‌کند تا پایداری سیستم‌های مختلف را ارزیابی کرده و ارتباط آن را با طراحی کنترل‌کننده‌های کارآمد درک کنند. همچنین، پیاده‌سازی عملی این مفاهیم در متلب به عنوان بخشی از این جلسه ارائه شده است.

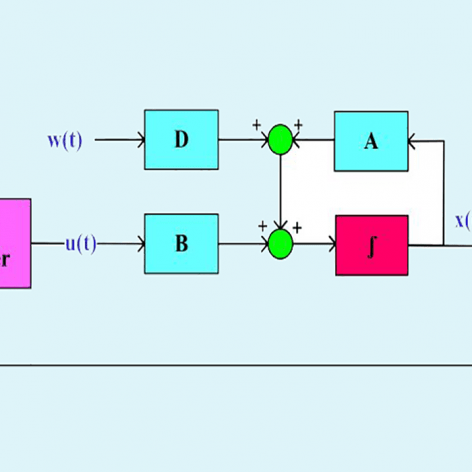
جلسه های ششم: ادامه پایداری و تحقق های فضای حالت

در این جلسه، به تکمیل مبحث پایداری سیستم‌های مرتبه کسری پرداخته می‌شود و موضوعاتی مانند تحلیل دقیق‌تر پایداری سیستم‌های پیچیده مورد بررسی قرار می‌گیرد.  سپس،  مفهوم تحقق‌های فضای حالت  (State- space Realization) برای سیستم‌های مرتبه کسری معرفی می‌شود. این تحقق‌ها ابزاری کارآمد برای نمایش سیستم‌های دینامیکی مرتبه کسری در قالب معادلات فضای حالت هستند که امکان تحلیل، شبیه‌سازی، و طراحی کنترل‌کننده‌ها را به‌صورت مؤثرتری فراهم می‌کنند. در این جلسه، روش‌های مختلف تحقق فضای حالت ارائه می‌شوند.

جلسه های هفتم: سیستم های مرتبه کسری گسسته زمان وتحلیل پایداری آنها

مفهوم سیستم‌های مرتبه کسری گسسته زمان (Discrete- time fractional-order  systems)  محتوای اصلی این جلسه می باشد که گسترشی از سیستم‌های مرتبه کسری پیوسته به دنیای گسسته هستند. این سیستم‌ها برای مدل‌سازی و کنترل فرآیندهایی که ذاتاً در زمان‌های گسسته رخ می‌دهند یا به دلیل محدودیت‌های سخت‌افزاری در نمونه‌برداری پیاده‌سازی می‌شوند، بسیار کاربردی‌اند. در ادامه، روش‌های مختلف تحلیل پایداری سیستم‌های گسسته مرتبه کسری مورد بحث قرار می‌گیرد.

جلسه های هشتم: کنترل پذیری و رویت پذیری سیستم های مرتبه کسری و آشنایی با کنترل کننده های PID  مرتبه کسری

در این جلسه، به بررسی دو ویژگی اساسی سیستم‌های دینامیکی، یعنی کنترل‌پذیری (Controllability) و رویت‌پذیری (Observability)، در سیستم‌های مرتبه کسری پرداخته می‌شود. این ویژگی‌ها تعیین می‌کنند که آیا می‌توان یک سیستم مرتبه کسری را با اعمال ورودی‌های مناسب کنترل کرد یا وضعیت داخلی آن را از طریق خروجی‌ها مشاهده نمود. مفاهیم کنترل‌پذیری و رویت‌پذیری در فضای حالت برای سیستم‌های مرتبه کسری بررسی شده و روش‌های تحلیل آن‌ها ارائه می‌گردد. در بخش دوم جلسه، با کنترل‌کننده‌های PID مرتبه کسری (Fractional-Order PID Controllers) آشنا می‌شویم. این کنترل‌کننده‌ها با افزودن انعطاف‌پذیری بیشتر به تنظیمات کنترلی کلاسیک، به‌ویژه برای سیستم‌های پیچیده و غیرخطی، عملکرد بهتری ارائه می‌دهند. نحوه  پیاده سازی این کنترل‌کننده‌ها، همراه با تحلیل تأثیر پارامترهای کسری بر عملکرد سیستم، توضیح داده می‌شود. در پایان، مثال‌هایی از شبیه‌سازی سیستم‌های مرتبه کسری و پیاده‌سازی کنترل‌کننده‌های FOPID در متلب ارائه شده است.

جلسه های نهم و دهم: طراحی کنترل کننده مرتبه کسری PI  (FOPI)

در جلسات نهم و دهم، طراحی مجموعه‌ای پایدارساز از کنترل‌کننده‌های مرتبه کسری PIیا FOPI ارائه می‌شود. این طراحی که بر اساس مقالات و پژوهش‌های منتشرشده در ژورنال‌های معتبر صورت گرفته است، از روش تحلیل D– Decomposition  بهره می‌برد. این روش یک ابزار قدرتمند گرافیکی برای تعیین محدوده‌های پایدار در فضای پارامترهای کنترل‌کننده است و امکان طراحی دقیق و سیستماتیک مجموعه‌ای از کنترل‌کننده‌ها را فراهم می‌کند. با استفاده از روشD-Decomposition، مرزهای پایداری در فضای پارامترهای کنترل‌کننده FOPI شناسایی شده و اثر تغییرات پارامترهای کسری بر عملکرد سیستم تحلیل می‌شود. این رویکرد به کاربران کمک می‌کند تا بتوانند مجموعه‌ای از کنترل کننده پایدارساز طراحی کنند. در کنار تبیین تئوری، شبیه‌سازی‌های گسترده و مثال‌های زیادی با استفاده از محیط متلب ارائه  شده است تا درک این مفاهیم و کاربرد آن‌ها در مسائل واقعی تسهیل گردد.

جلسه های یازدهم: طراحی کنترل کننده مرتبه کسری (FOPID) PID

در جلسه یازدهم، طراحی کنترل‌کننده‌های مرتبه کسری FOPID و PID به‌طور جامع مورد بررسی قرار می‌گیرد. این طراحی، که بر اساس پژوهش‌های معتبر منتشرشده در ژورنال‌های تخصصی صورت می‌گیرد، از روش تحلیل D-Decomposition به‌عنوان ابزاری قدرتمند برای بررسی محدوده‌های پایداری در فضای پارامترهای کنترل‌کننده استفاده می‌کند. این روش گرافیکی امکان تحلیل دقیق مرزهای پایداری و تأثیر تغییرات پارامترهای کسری بر عملکرد سیستم را فراهم می‌آورد. در این جلسه، مفاهیم پایه‌ای و تئوری کنترل‌کننده‌های FOPID معرفی می‌شود و محدوده‌های پایداری آن‌ها در فضای پارامترها تحلیل می‌گردد. با استفاده از ابزارهای پیشرفته شبیه‌سازی مانند MATLAB، شبیه‌سازی‌های گسترده‌ای ارائه شده و ارزیابی می‌شود. این رویکرد به طراحان کمک می‌کند تا کنترل‌کننده‌هایی با عملکرد پایدار و بهینه طراحی کنند. در کنار مباحث تئوری، مثال‌های کاربردی نیز ارائه می‌شود تا درک این مفاهیم و کاربرد آن‌ها در مسائل واقعی تسهیل گردد.

جلسه های دوازدهم: طراحی کنترل کننده های مرتبه کسری  (FOPID-FOPI-FOPD) برای سیستم های با تاخیر زمانی

 در جلسه دوازدهم، طراحی کنترل‌کننده‌های مرتبه کسری مانند FOPID، FOPI و FOPD برای سیستم‌های دارای تأخیر زمانی مورد بررسی قرار می‌گیرد. این جلسه به تحلیل پایداری و عملکرد این کنترل‌کننده‌ها با استفاده از ابزارهای پیشرفته نظیر روش D-Decomposition می‌پردازد. این روش قدرتمند گرافیکی، امکان تعیین محدوده‌های پایداری در فضای پارامترهای کنترل‌کننده را فراهم می‌کند و به طراحان اجازه می‌دهد تأثیر تغییرات پارامترهای کسری و تأخیر زمانی را به‌دقت تحلیل کنند. در کنار بررسی مفاهیم تئوری، شبیه‌سازی‌های عملی با MATLAB و مثال‌های کاربردی ارائه می‌شود تا فرآیند طراحی کنترل‌کننده‌های پایدار و بهینه تسهیل گردد.

جلسه سیزدهم: طراحی کنترل کننده های مرتبه کسری  (FOPID-FOPI-FOPD) برای ساختار پیشبین اسمیت

در جلسه سیزدهم، طراحی کنترل‌کننده‌های مرتبه کسریFOPID، FOPI، FOPD برای سیستم‌های دارای تأخیر زمانی و ساختار پیش‌بین اسمیت مورد بررسی قرار می‌گیرد. این جلسه به تحلیل پایداری و عملکرد این کنترل‌کننده‌ها در ترکیب با پیش‌بین اسمیت می‌پردازد، که یکی از مؤثرترین روش‌ها برای جبران تأخیر زمانی در سیستم‌های کنترلی است. با استفاده از ابزارهای گرافیکی پیشرفته مانند روش D-Decomposition، محدوده‌های پایداری در فضای پارامترهای کنترل‌کننده تعیین می‌شود و تأثیر پارامترهای مرتبه کسری و تأخیر زمانی به‌صورت دقیق تحلیل می‌گردد. علاوه بر بررسی مفاهیم تئوری، شبیه‌سازی‌های عملی با نرم‌افزار MATLAB و ارائه مثال‌های کاربردی به‌منظور تسهیل فرآیند طراحی کنترل‌کننده‌های پایدارساز انجام می‌شود. این جلسه، رویکردی جامع برای بهبود عملکرد سیستم‌های تأخیری از طریق ترکیب کنترل‌کننده‌های مرتبه کسری و ساختار پیش‌بین اسمیت ارائه می‌دهد.

جلسه چهاردهم: طراحی کنترل کننده های مرتبه کسری برای سیستم های قدرت (کنترل فرکانس بار) به همراه چند نکته تکمیلی برای طراحی

در این جلسه، به بررسی روش‌های طراحی کنترل‌کننده‌های مرتبه کسری (Fractional-Order Controllers) برای بهبود عملکرد سیستم‌های قدرت و کنترل فرکانس بار پرداخته شده است. یکی از روش‌های کلیدی مورد استفاده در این آموزش، روش D-decomposition است که برای تعیین ناحیه پایداری کنترل‌کننده‌های مرتبه کسری به کار گرفته شده است. این روش با تحلیل و تعیین مرزهای پایداری در فضای پارامترهای کنترل‌کننده، امکان طراحی مطمئن را فراهم می‌کند. علاوه بر این، در این آموزش ناحیه پایداری برای کنترل‌کننده‌های FOPD (Fractional-Order Proportional-Derivative) نیز به دست آمده و تحلیل شده است، که به مهندسان و طراحان کمک می‌کند تا کنترل‌کننده‌هایی با عملکرد پایدار و کارآمد طراحی کنند.

جلسه پانزدهم: کنترل مقاوم مرتبه کسری: تئوری خاریتانوف (Kharitonov theorem)  و پایه های کنترل مقاوم مرتبه کسری

در این جلسه، تئوری خاریتانوف به عنوان یکی از ابزارهای قدرتمند در تحلیل پایداری سیستم‌های نامعین (سیستم‌هایی که پارامترهای آنها در بازه‌ای مشخص تغییر می‌کنند) مورد بررسی قرار می‌گیرد. این تئوری با ارائه چهار چندجمله‌ای خاص، امکان بررسی پایداری سیستم‌های نامعین را فراهم می‌کند و به طراحان کمک می‌کند تا کنترل‌کننده‌هایی طراحی کنند که در برابر تغییرات پارامترهای سیستم مقاوم باشند. همچنین، در این جلسه علاوه بر تئوری خاریتانوف، قضیه Zero Exclusion Principle نیز مطرح می‌شود. این قضیه یکی از ابزارهای مهم در تحلیل پایداری سیستم‌های نامعین است و به ویژه در کنترل مقاوم مرتبه کسری کاربرد دارد. بر اساس این قضیه، اگر مجموعه‌ای از چندجمله‌ای‌ها (که نمایانگر سیستم‌های نامعین هستند) شامل مبداً نباشند و حداقل یک چندجمله‌ای پایدار در این مجموعه وجود داشته باشد، آنگاه تمام سیستم‌های نامعین در این مجموعه پایدار خواهند بود. این اصل به طراحان کمک می‌کند تا با بررسی رفتار سیستم در مرزهای پایداری، مقاومت سیستم در برابر تغییرات پارامترها را تضمین کنند.

جلسه های شانزدهم تا بیستم: کنترل مقاوم مرتبه کسری: تحلیل پایداری مقاوم چند جمله ای های مرتبه کسری با نامعینی بازه ای (پارامتری)

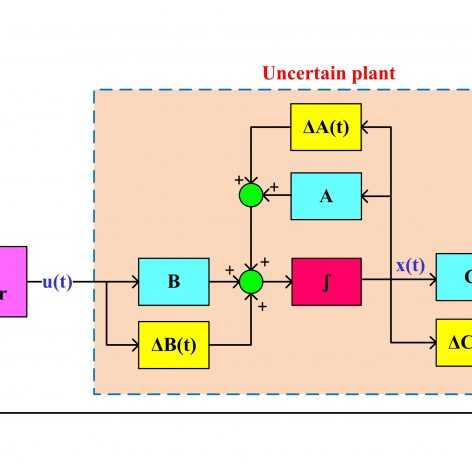
در این جلسات، مباحث پیشرفته‌تر و عمیق‌تری در حوزه کنترل مقاوم مرتبه کسری مورد بررسی قرار می‌گیرد. تمرکز اصلی بر تحلیل پایداری مقاوم چندجمله‌ای‌های مرتبه کسری است که با نامعینی بازه‌ای (Interval Uncertainty)  در پارامترهای سیستم مواجه هستند. این نامعینی به این معناست که پارامترهای سیستم در بازه‌های مشخصی تغییر می‌کنند و سیستم باید در تمام این بازه‌ها، پایداری خود را حفظ کند. برای تحلیل پایداری چنین سیستم‌هایی، از قضیه Zero Exclusion Principle به عنوان یک ابزار قدرتمند استفاده می‌شود. این قضیه با بررسی رفتار سیستم در مرزهای پایداری، به طراحان کمک می‌کند تا مقاومت سیستم در برابر تغییرات پارامترها را تضمین کنند. علاوه بر این، در این جلسات، روش‌های عددی و تحلیلی برای بررسی پایداری چندجمله‌ای‌های مرتبه کسری با نامعینی بازه‌ای ارائه می‌شود. این روش‌ها به مهندسان و پژوهشگران این امکان را می‌دهند تا کنترل‌کننده‌های مقاوم و پایدار طراحی کنند که در شرایط نامعین نیز عملکرد بهینه‌ای داشته باشند. این مباحث نه تنها درک عمیق‌تری از تحلیل و طراحی سیستم‌های کنترل مقاوم مرتبه کسری فراهم می‌کنند، بلکه کاربردهای گسترده‌ای در حوزه‌های مختلف مهندسی، از جمله سیستم‌های قدرت، رباتیک و سایر سیستم‌های دینامیکی دارند.

جلسه بیستم یکم: کنترل مقاوم مرتبه کسری: تحلیل پایداری مقاوم سیستم های مرتبه کسری با نامعینی بازه ای (پارامتری) با استفاده از FOMCON

در این جلسه، ابتدا تحلیل پایداری مقاوم برای سیستم‌های مرتبه کسری به طور جامع و مفصل ارائه و تشریح می‌شود. سپس، از تولباکس FOMCON (Fractional-order Modeling and Control) به عنوان یک ابزار قدرتمند و کاربردی برای شبیه‌سازی و تحلیل سیستم‌های مرتبه کسری استفاده می‌شود. این تولباکس امکان تحلیل پایداری مقاوم سیستم‌ها و چندجمله‌ای‌های مرتبه کسری را فراهم می‌کند و به طراحان کمک می‌کند تا در شرایط نامعین، سیستم‌هایی پایدار و مقاوم طراحی کنند.  برای درک بهتر مفاهیم پایداری مقاوم و تسلط بیشتر بر استفاده از این تولباکس، مثال‌های متعددی در طول جلسه ارائه می‌شود. این مثال‌ها به شرکت‌کنندگان کمک می‌کند تا با کاربردهای عملی تحلیل پایداری مقاوم و نحوه استفاده از FOMCON در پروژه‌های واقعی آشنا شوند. این جلسه نه تنها درک عمیق‌تری از مفاهیم کنترل مقاوم مرتبه کسری ایجاد می‌کند، بلکه مهارت‌های کاربردی را برای تحلیل و طراحی سیستم‌های پیچیده در اختیار مهندسان و پژوهشگران قرار می‌دهد.

مطالعه بیشتر