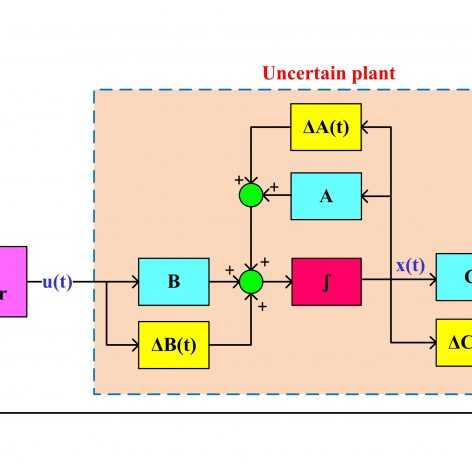
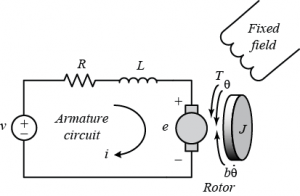
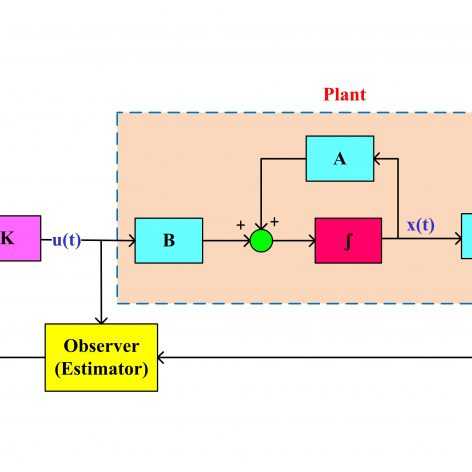
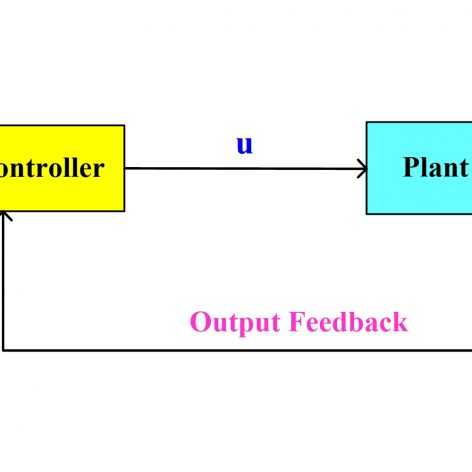
در سری فیلمهای قبلی موجود در سایت به صورت جداگانه کنترل مقاوم سیستمهای خطی تحت نامعینی پارامتری با فیدبک حالت و کنترل فیدبک خروجی سیستمهای خطی بدون نامعینی مورد بررسی قرار گرفتند. ممکن است شرایط سیستم به گونه ای باشد که هم نامعینی پارامترهای سیستم قابل ملاحظه بوده و هم اندازه گیری تمام حالتها از طریق سنسور امکان پذیر نباشد. در این موقعیتها امکان استفاده از روشهای فوق وجود ندارد و باید ساختار کنترل کننده اصلاح شود. در این سری جلسات، یک کنترل کننده مقاوم دینامیک برای سیستمهای خطی تحت نامعینی پارامتری به گونهای طراحی میشود که فقط از خروجی (یا خروجی های) سیستم برای کنترل استفاده میکند و نیازی به تمام حالتها ندارد. لازم به ذکر است که با استفاده از رویتگرهای مرسوم لیونبرگر این مساله قابلیت تبدیل به LMI را نداشته و بنابراین از یک کنترل کننده دینامیک دیگر استفاده شده است و مساله طراحی این کنترل کننده به چند نامساوی ماتریسی خطی تبدیل شده است. در انتها برای ارزیابی عملکرد، این کنترل کننده به همراه یک کنترل کننده فیدبک خروجی غیر مقاوم (با استفاده از رویتگر لیونبرگر) بر روی مدل خطی یک موتور DC پیاده شده و تحت پروفایلهای مختلف نامعینی از جمله نامعینی های ثابت، سینوسی و تصادفی عملکرد هر دو سیستم کنترل مورد بررسی قرار گرفته است. همچنین علاوه بر رگولاسیون، مسایل ردیابی و تحلیل پاسخ فرکانسی هر دو سیستم حلقه بسته بررسی شده و خواص تضعیف نویز و پهنای باند سیستم در شبیهسازی ها برای دو روش فوق باهم مقایسه شدهاند. لازم به ذکر است که بنابه درخواست مکرر شما عزیزان شبیهسازیها هم به صورت کد انجام شده و هم در محیط سیمولینک.
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
فرمولبندی طراحی کنترل مقاوم فیدبک خروجی برای سیستمهای دارای نامعینی پارامتری
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
پیادهسازی کنترلکننده مقاوم بر روی دینامیک خطی موتور DC و شبیهسازی در متلب
شبیهسازی در محیط سیمولینک و تحلیل در حوزه فرکانس
جلسه دوم:
جلسه سوم:
جلسه چهارم:
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



امین
سلام آقای دکتر. بابت آموزش های بی نظیرتان سپاس گزارم.
من با سیستمی مواجه شده ام که LPV است، با در نظر گرفتن نامعینی پلی توپ، مساله پایدار سازی را حل کرده ام.
در رابطه ماتریس های کنترل کننده، ماتریس های سیستم وجود دارد که وابسته به پارامتر است.
آیا می توانم با در نظر گرفتن مقادیر نامی پارامترهای متغیر، ماتریس های کنترل کننده نهایی را به دست آورم؟
ممنون می شوم راهنمایی بفرمایید.
با سپاس فراوان
علی جوادی
خیر
ایمان
سلام آقای دکتر. وقت شما بخیر. ممنون از آموزش های بسیار خوبتان.
سوالی داشتم از خدمتتان.
در این دوره، تعداد حالت های کنترل کننده برابر با تعداد حالت های سیستم در نظر گرفته شده است. آیا می توان تعداد حالت ها را با همین روش کم تر هم در نظر گرفت؟
با تشکر
علی جوادی
سلام
با روشی که در این مجموعه استفاد شده خیر ولی برای حالتی که گفتید روشهایی در مقالات هست که میتونید مراجعه کنید
ایمان
سپاسگزارم بابت وقتی که گذاشتید.
من مجموعه های LMI که شما تدریس کرده اید را خریداری کرده و به طور کامل دیده ام، مقالاتی که تعداد حالت های کنترل کننده را کمتر در نظر گرفته باشند و مشابه روش تدریس شده شما باشد را اگر سراغ دارید، امکانش هست معرفی بفرمایید؟
با تشکر از زحمات شما استاد گرامی
علی جوادی
در این مورد من سرچ نکردم ولی قبلا دیدم مقالاتی که فیدبک خروجی با شرایطی که گفتید داشتند و از LMI استفاده کردند
احسان
سلام اقای دکتر. ممنون از آموزش بسیار خوبتان.
سوالی داشتم از خدمتتان.
اگر A و B دو ماتریس باشند و داشته باشیم:
A>B
این به چه معناست؟
یعنی همه مقادیر ویژه A بزرگتر از B هستند؟
ممنون می شوم راهنمایی بفرمایید.
علی جوادی
سلام
اگر A>B باشد، یعنی A-B یک ماتریس مثبت معین بوده و تمام مقادیر ویژه آن مثبت هستند.
حسین
سلام اقای جوادی
ممنون بابت توضیحاتتون من ویدئوهای طراحی کنترلر فیدبک حالت مقاوم با نامعینی (جلسات 1، 2، 3 و 6) و نامعینی همراه با اغتشاش (جلسات 1 و 2) رو دیدم
چند تا سوال خدمتتون داشتم:
1- تو این مسائلی که ما داشتیم اصلا بحثهای پاسخ گذرا مثل rise time، پهنای باند سیستم، محل مطلوب قطبهای سیستم حلقه بسته مطرح نشدن
الان با توجه به توضیحات دروس شما،
من متوجه شدم مثلا سیستم پایداره و خطای حالت دائم صفر داره،
حالا کجا میتونم خواسته های طراحی مثل پهنای باند و …. رو در مساله بگنجونم.
2- در مساله ی ردیابی با وجود اغتشاش، اگر ورودی مرجع سیسنوسی باشه، خیلی خطای حالت دائم ایجاد میشد که دیگه استفاده از این کنترلر رو غیرقابل توجیه میکنه
چطور میشه در سیستمهای ردیابی با مرجع سینوسی این خطا رو کمتر کرد یا باید کلا بریم سمت روشهای طراحی دیگه
خیلی ممنون
براتون ارزوی موفقیت و سلامت دارم
علی جوادی
@حسین,
با سلام و تشکر از لطف شما
1) همونطور که اشاره کردید در این فیلمها به خیلی از معیارهای حوزه زمان و فرکانس پرداخته نشده و فقط مباحث پایه کنترل مقاوم ذکر شده. امیدوارم در آینده فرصت بشه تا به این موضوعات هم بپردازم. البته بعضی از این موارد در مبحث کنترل مقاوم نمیگنجه. برای اطلاعات بیشتر در این زمینه به مقاله زیر مراجعه کنید:
https://ieeexplore.ieee.org/document/599969
2) در این سری فیلمها نحوه بهبود پهنای باند مطرح نشده. با تبدیل این معیار به LMI میشه پهنای باند رو افزایش داد و در نتیجه سرعت عمل سیستم بیشتر شده و ورودی های مرجع سریعتر دنبال میشه. البته در هر صورت یه فرکانسی هست که از اون به بعد دیگه خطای ردیابی زیاد میشه
حسین
خیلی ممنون بابت توضیحاتتون
مشتاقانه منتظر فیلمهای و جلسات جدیدتون هستم.
موفق و پیروز باشید
محمد
سلام آقای دکتر وقتتون بخیر
سیستم بنده یک سیستم MISO هستش و واسه ردیابی سیگنال رفرنس ، وقتی معادله (An*xr+Bn*ur) رو حل میکنم ur بر حسب yr , xr بدست میاد.میخواستم ببینم واسه پیاده سازی xr رو چه جوری بدست بیارم؟
علی جوادی
@محمد,
سلام
ورودی مرجع xr توسط طراح و طبق خواسته شما از سیستم تعیین میشه و از جایی بدست نمیاد
محمد
سلام اقای دکتر
شما تو این اموزش و سایر اموزش های کنترل مقاوم سیستم هایی که روش هاتون رو روش پیاده کردید یک سرس سیستم هایی هستن که از طریق قوانین فیزیکی مدل شدند و در نتیجه شما عدم قطعیت ها رودر پارامترهای فیزیکی سیستم در نظر گرفتید، میخواستم ببینم که ایا این روش ها روی سیستم مد نظر من که مدلسازی اون باید از طریق شناسایی سیستم صورت بگیرد قابل پیاده سازی است؟
با تشکر
علی جوادی
@محمد,
سلام
مهم نیست که منشا نامعینی چی باشه. مهم اینه که شما بتونید نامعینی رو به شکل نرم محدود (به شکل گفته شده در فیلمها) مدل کنید. حالا ممکنه این نامعینی ناشی از عدم قطعیت در پارامتر فیزیکی سیستم باشه یا اینکه خطای مدلسازی در فرایند شناسایی باشه
محمد
@علی جوادی,
سلام
اقای دکتر پروژه بنده در مورد کنترل بهینه تولید نفت با استفاده از شناسایی مدل و تخمین عدم قطعیت هستش، که به احتمال زیاد باید از تکنیک کنترلی مقاوم استفاده کنم. میخواستم ببینم کدوم فیلم های اموزشی موجود در سایت رو پیشنهاد میکنین که تهیه کنم و اگه منبع دیگه ای مدنظرتون هست که میتونه کمکم کنه رو بفرمایید.
خیلی خیلی ممنون میشم.
علی جوادی
@محمد,
سلام
اول باید تعیین کنید که سیستم شما خطی هست یا نه، چون تمام روشهای گفته شده در سایت برای سیستمهای خطی هستند.
در مرحله بعد باید ببینید در سیستم نامعینی دارید یا اغتشاش یا هر دو. همچنین انتخاب کنید که فیدبک حالت نیاز دارید یا خروجی. بعد میتونید با دیدن کلیپ کوتاه زیر، مجموعه آموزشی مورد نظر رو انتخاب کنید:
http://www.aparat.com/v/cD2Ii
محمد
@علی جوادی,
خیلی ممنون اقای دکتر
مدیر سایتادمین سایت
@محمد,
موفق باشید
مجتبی
با سلام امکان داره بنده ایمیل شما را جهت پرسش برخی سوالهایم داشته باشم؟ زمینه تز بنده شبیه کار شماست.
ممنون از شما
علی جوادی
سلام. اقدام شد
مجتبی
متشکرم
رضا
سلام آقای دکتر جوادی
یه خدا قوت باید به شما بابت این همه آموزش توی سال 95 گفت . امیدوارم سال 96 هم برای شما پر خیر باشه هم برای ما پر از آموزش جدید
یه سوال از خدمتتون داشتم
وقتی میخواهیم حالت های یک سیستم حلقه باز به صورت x-dot = Ax+Bu رو به ورودی خاص رسم کنیم از شبیه سازی اویلر که توضییح دادید یا دستور lsim استفاده می کنیم
سوال بنده اینه که آیا در زمانیکه سیستم دارای اغتشاش هست و بصورت x-dot=Ax+Bu+Dw هست باید در شبیه سازی اثر جمله Dw هم باید حتما دیده بشه؟
البته شما در برنامه نویسی هاتون به روش اویلر اونرو لحاظ کردید و قاعدتا جواب این سوال مثبت هستش زیرا وقتی سیستم بصورت x-dot=Ax+Bu+Dw هست با n معادله دیفرانسیل جدید روبرو هستیم که قاعدتا جوابی که برای حالت ها بدست میاد با حالت x-dot = Ax+Bu باید تفاوت کنه. با این وجود میخوام نظر شما رو بدونم.
من روی یک سیستم مبدل DC-DC کار میکنم که بعلت سویچینگ با فرکانس بالا در مدار دو فضای حالت بدست میارن و در نهایت یک میانگین براش می گیرن. اما در مقالات دو روش برای بیان اغتشاش وجود داره اکثرا بصورت x-dot=Ax+Bu+Dw در نظر گرفتن که اگر اثر جمله Dw رو در نظر بگیریم ، مدل فضای حالت به هیچ عنوان با نتایج سیمولینک مدار در متلب سازگار نیست و خروجی مدار متفاوت خواهد بود (البته اگر جمله Dw رو در شبیه سازی در نظر نگیریم نتیجه درست میشه اما فکر نکنم که مجاز به حذف جمله Dw باشیم) . عده قلیلی هم سیستم رو به صورت x-dot = Ax+Bu در نظر گرفتن و اثر جملات اغتشاشی رو به صورت نامعینی پارامتری در ماتریس B جای دادن که کاملا با نتایج سیمولینک مدار سازگاره. تفاوت در دیدگاه در مقالات منو به شک انداخته و برای روشن شدن موضوع مزاحم شما شدم.
پیشاپیش هم سال نو رو به شما تبریک میگم و آرزوی موفقیت دارم براتون .
علی جوادی
@رضا,
با سلام و تشکر از لطف شما
اگر در مدل میانگین اغتشاش حضور داشته باشه اصولا باید در نظر گرفته بشه و گرنه همونطور که گفتید با سیستم بدون اغتشاش تفاوتی نخواهد داشت.
البته در مورد سیستمهای سویچینگ اطلاعات من خیلی کمه و نمیتونم در این مورد اظهار نظر قطعی بکنم. برای اطلاعات بیشتر از خانم دکتر فرجی که آموزشهای سیستمهای سویچینگ و مارکوف رو انجام میدهند، کمک بگیرید
سال نوی شما هم پیشاپیش مبارک و موفق باشید
رضا
@علی جوادی,
ممنون از پاسخگویی شما
جوابم رو گرفتم ، پس برای شبیه سازی سیستم x-dot=Ax+Bu+Dw حتما باید اثر جمله Dw رو تو شبیه سازی (چه با روش اویلر و چه با روش چه دستور lsim) در نظر گرفته بشه تا تفاوتش با سیستم x-dot=Ax+Bu مشخص باشه
ممنون از راهنماییتون