آموزش مد لغزشی طبق کتاب اسلوتین
در این پست فیلم آموزش مد لغزشی طبق کتاب اسلوتین قرار داده میشود. کتاب اسلوتین رو اگه خونده باشید متوجه خواهید شد که بسیاری از مطالب این فصل گنگ هستند و نیاز به توضیحات بیشتر دارن. ضمن اینکه به نظر من بعضی از مطالب این کتاب بعد از اینکه فصل به پایان رسید باید باز هم در موردشون بحث بشه اما توی کتاب این امکان وجود نداره . از طرفی مثال هایی در این کتاب وجود داره که اگه با روند شبیه سازی اون ها هم آشنا بشیم در یادگیری این روش جذاب بسیار موثره. من مد لغزشی رو بارها و بارها بر روی سیستم های مختلف شبیه سازی کردم و مقالات زیادی در این زمینه کار کردم.
چیزی که من تضمین میدم اینه که بعد از این دوره آموزشی، به نتایج زیر خواهید رسید:
مد لغزشی رو به طور کامل و فراتر از مطالب کتاب درک خواهید کرد
با نحوه شبیه سازی مثال ها و بحث روی آنها کاملا آشنا خواهید شد
نحوه تلفیق این روش با روش هایی مثل فازی، ژنتیک و … رو خواهید آموخت (مد لغزشی فازی در همین سایت قرار داده شده است برای دانلود این فیلم آموزشی کلیک بفرمایید)
پیاده سازی این روش بر روی سیستم های غیرخطی پیچیده و شبیه سازی آنها رو یاد خواهید گرفت.
میتونید برای سیستم خودتون این شبیه سازی ها رو انجام بدید
مقالات مختلف رو که در زمینه مد لغزشی هستن میتونید براحتی درک کنید.
تفاوت این آموزش با آموزش دیگری تحت عنوان “آموزش مد لغزشی از طراحی تا شبیه سازی“ که در سایت قرار داده شده در این هست که آموزشی که در این پست قرار داره برای افرادیه که میخوان با عمق بیشتری مد لغزشی رو یاد بگیرن و اون آموزش برای کسیه که اطلاعات بسیار ناچیزی از مد لغزشی داره و فقط میخواد روی یه سیستم ساده یک مد لغزشی ساده رو پیاده کنه. اما در اینجا هم با مباحث بیشتری آشنا خواهید شد و هم مطالب با عمق بیشتری ذکر خواهند شد. همچنین یک “جزوه کاربردی مد لغزشی“ نیز در این سایت قرار داده شده است که همونطور که از اسمش معلومه فقط حالت کاربردی داره.
جلسه اول:
مقدمات و تبدیل مسئله مرتبه n به مسئله مرتبه یک
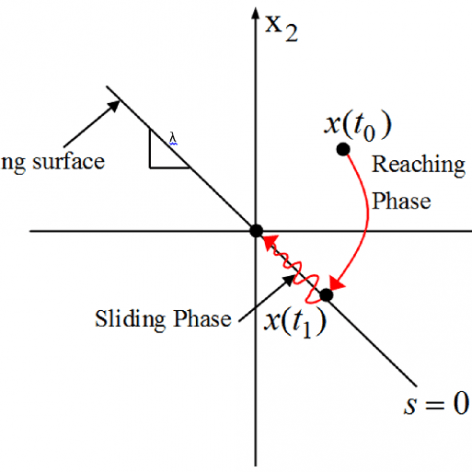
در این جلسه در مورد صورت مسئله مد لغزشی، انواع نامعینی، سطوح لغزشی و از همه مهمتر تبدیل مسئله مرتبه ان به مسئله مرتبه یک در مد لغزشی پرداخته شده است. در ادامه کلا در ارتباط با اینکه چطور میتوان یک مسئله ردیابی مرتبه ان رو به یک مسئله پایدارسازی از مرتبه یک (سطح سوئیچینگ) تبدیل کرد بحث کرد.
مدت زمان آموزش: 67 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس
جلسه دوم:
شرط لغزشی ، فیلیپف دینامیک معادل
مبحث ناتمام جلسه قبل در این جلسه به اتمام میرسد. سپس در مورد شرط لغزش به طول مفصل بحث میشود همچنین در ادامه پدیده چترینگ توضیح داده شده است و در نهایت به توضیح فیلیپف و دینامیک معادل پرداخته شده است. دقت کنید این مطلب در کتاب اصلا بخوبی تفسیر داده نشده است.
مدت زمان آموزش: 55 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس
جلسه سوم:
نحوه طراحی و شبیه سازی مد لغزشی به صورت گام به گام
در این جلسه ابتدا یک الگوریتم برای طراحی مد لغزشی ارائه شده است. این الگوریتم به صورت واضح بیان شده است و به صورت مفصل در مورد آن بحث شده است. مباحثی از قبیل نحوه انتخاب سطح لغزش، چرا سطح لغزش به فرمی که در کتاب است در نظر گرفته می شود؟ چرا در همه مقالات به این فرم نیست و ….. و در ادامه با یک مثال تک ورودی و تک خروجی ابتدا طراحی به طور کامل و براساس الگوریتمی که در ابتدای جلسه گفته شد انجام میشود و سپس این مثال در نرم افزار MATLAB شبیه سازی شده است. و در پایان، به بحث در مورد پارامتر های طراحی در این نرم افزار پرداخته شده است.
مدت زمان آموزش: 55 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس و ام فایل مربوط به درس
جلسه چهارم:
طراحی و شبه سازی مد لغزشی برای سیستم های مرتبه دو و سه
در این جلسه طراحی کنترل کننده مد لغزشی و شبیه سازی آن در نرم افزار MATLAB برای دو سیستم مرتبه دو و سه انجام شده است. یکی از بحث های مهم طراحی مد لغزشی یعنی تبدیل هر سیستم غیرخطی به سیستم مرتبه دوم استاندارد به طور مفصل بحث شده است. همچنین مباحث تکمیلی در مورد تعریف سطح لغزش در مثال مربوط به سیستم مرتبه سه ذکر شذه است.
مدت زمان آموزش: 66 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس و 2 ام فایل مربوط به درس
جلسه پنجم:
کنترل انتگرالی ، حد بهره
در ابتدای جلسه، کنترل کننده مد لغزشی برای سیستم های مرتبه n طراحی شده است تا اگر سیستم شما مثلا دارای درجه نسبی ده بود دیگه از اول تا آخر طراحی رو انجام ندید و یا اینکه اگه میخواید طراحی رو انجام بدید بدونید میخواید به چه چیزی برسید. در ادامه به بحث در مورد کنترل انتگرالی و حد بهره پرداخته شده است. توی کتاب دلیل استفاده از کنترل انتگرالی و اینکه چرا باید سطح لغزش در ابتدا صفر باشد چیزی نگفته. از طرفی مثال هم حل نشده است. ما در این آموزش هم کاربرد کنترل انتگرالی رو گفتیم و هم یک مثال رو در نرم افزار متلب شبیه سازی کردیم. پس از اون، به نقطه اوج طراحی مد لغزشی یعنی برای سیستم هایی که به فرم x^(n)=f(x)+g(x)u هستند پرداخته شده است. نحوه اثبات در کتاب خیلی گنگه. این اثبات با تمام جزئیات از ابتدا تا انتها ذکر شده است.
مدت زمان آموزش: 66 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس و ام فایل مربوط به درس
جلسه ششم:
چترینگ و راههای حذف آن (1)
در ابتدا به طراحی یک مثال برای سیستمی که بهره داشته باشه پرداخته شده است. سپس وارد موضوع چترینگ شدیم. کاربردهای چترینگ، نحوه حذف چترینگ در حالت کلی، دسته بندی که برای حذف چترینگ برای حالت های مختلف میتوان انجام داد و شبیه سازی یک مثال برای حالتی که لایه مرزی ثابت باشد موضوعاتیست که در این جلسه کار شده است. برای حذف چترینگ دو دسته بندی کلی انجام شده است یکی حذف چترینگ برای سیستم هایی که باید در آنها لایه مرزی ثابت باشد و دیگری حذف چترینگ برای سیستم هایی که در آنها لایه مرزی متغیر بهتر از لایه مرزی ثابت جواب می دهد. در این جلسه به دسته بندی اول پرداخته شده است.ضمنا مثالی که در این جلسه شبیه سازی شده است مثال7-2 کتاب است.
مدت زمان آموزش: 53 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس و ام فایل مربوط به درس
جلسه هفتم:
چترینگ و راههای حذف آن (2)
در این جلسه به راه حل جذف چترینگ با استفاده از لایه مرزی متغیر پرداخته شده است. این روش برای سیستم هایی که ضریب ورودی کنترلی در آنها یک هست و نیست بررسی شده است و با ذکر مثال و شبیه سازی آن در نرم افزار متلب به صورت مفصل بحث شده است. حذف چترینگ با استفاده از لایه مرزی متغیر با زمان برای سیستم های خاصی هست. پیشنهاد می شود در صورتیکه فقط می خواید این جلسه رو خریداری بفرمایید جلسه قبل رو هم تهیه کنید چون ممکنه برای سیستم شما استفاده از این روش موضوعیت نداشته باشد.
مدت زمان آموزش: 55 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس و ام فایل مربوط به درس
جلسه هشتم:
طراحی مد لغزشی برای یک سیستم چند ورودی – چند خروجی
یک مثال جامع که تمامی مباحث قبل رو بتونه پوشش بده رو طراحی کردم. مد لغزشی با در نظر گرفتن تمامی جوانب برای این سیستم طراحی شده است. در این مثال، یک سیستم دو ورودی و دو خروجی که چهار متغیر حالت دارد در نظر گرفته شده است. محدودیت های لامبدا نیز در صورت سوال مطرح شده است و این موضوع در ابتدای جلسه بحث شده است که چطور می توان محدودیت های مختلف را بر روی پارامتر لامبدا اعمال کرد.توجه بفرمایید این جلسه آخرین جلسه از مجموعه آموزش های مد لغزشی بر اساس کتاب اسلوتین بود. در ادامه سعی دارم نحوه تلفیق این روش با روش های دیگر و انواع دیگر مد لغزشی رو برای شما آماده کنم.
مدت زمان آموزش: 54 دقیقه
محتویات دانلود : فیلم، پاورپوینت درس
جلسه نهم:
در اين جلسه، يک واسط گرافيکي در متلب (gui) توليد شده که با استفاده از آن به طور اتوماتیک مي توانید يک کنترل کننده مد لغزشی (Sliding Mode) براي يک سيستم طراحي کنید. در واقع چکیده مباحث تدریس شده به صورت یک پنل تصویری در این جلسه آمده است. مخصوصاً برای دوستانی که فقط خروجی کار برای آنها مهم است، این واسط گرافيکي می تواند بسیار مفید باشد. این جلسه توسط آقای نورمحمدی فارغ التحصیل ارشد شریف تدریس شده است
برای خرید جلسه 9 به صورت جداگانه می توانید با کلیک بر روی دکمه خرید زیر این جلسه را نیز به سبد خریدتان اضافه کنید
جلسه 9 : طراحی مد لغزشی با استفاده از gui
|
۱۶۰,۰۰۰ تومان قیمت اصلی: ۱۶۰,۰۰۰ تومان بود.۱۱۷,۶۰۰ تومانقیمت فعلی: ۱۱۷,۶۰۰ تومان.Add to cart
|
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم





zoha
سلام ،ممنون از زحماتتون
من جلسه ششم از مد لغزشی رو تهیه کردم فقط پاورپونت و برنامه نویسی داخلش هست فیلم آموزشی نداره؟
مدیر سایتادمین سایت ( مالک تایید شده )
@zoha,
سلام
نظر لطف شماست
!!!
اینطوری نیست همه فایلها توشه. کسی تا الان اینو نگفته. دهها نفر اینو خریدن. حجم فایل رر هم گویای این هست. لطفا یه بار دیگه دانلود کنید. توی یه پوشه جداگانه قرار بدین
درود
امیرحسین
سلام استاد خوبید
1 – تو جلسه آخر همان روش تک ورودی رو برای حالت دو ورودی به کار بردید
می خواستم بپرسم این تعمیم همیشه و برای همه راه های کنترلی درسته یا شرایطی داره؟
یعنی واسه بردن به چند متغیره دانش زیادتری نیست؟
2 – واسه یک پرنده شش درجه آزادی که می خواهیم در صفحه حرکت کند باید کل شش معادله رو توی شبیه سازی قرار بدیم یا فقط معادلات x و y ؟
چون تو معادلات x و y مولفه های z , teta , phi, zeta که مربوط به زوایای چرخش و ارتفاع هستند رو هم داریم پش طبیعتا باید معادلاتش بیاد آیا درسته؟
آیا اونها نیاز به کنترلر دارند؟ یا باید مقدار مطلوبشون رو روی صفر تنظیم کنیم؟
3 – توجلسه آخر اگه تو ده دقیقه کد رو هم می نوشتید فیلم تون کامل میشد؟ به نظرتون کامل بودن مهمه یا حجم کمتر شدن؟چون واقعا حیفه حالا 70 مگ بشه 90 مگ مگه فرقی داره؟
4- اگه تو معادله دو ورودی داشته باشیم باید وروی رو چی در نظر بگیریم؟(x1.. یعنی مشتق دوم x1 و هم چنین u1. یعنی مشتق اول u1)
X1..=f+2u1.+u1+au2.+u2
X2..=f2+u2.+u1.+u2
ممنون
مدیر سایتادمین سایت ( مالک تایید شده )
@امیرحسین,
سلام
1-نود درصد اوقات همین روشه. ده درصد دیگه باید مینیمم فاز بودن سیستم هم بررسی بشه ( که اکثرا مینیمم فاز هستن)
2- کلشو باید قرار بدین اما اگه معادلاتتون فقط براساس ایکس و وای هستش میتونید فقط همین دوتا رو قرار بدین. (پیشنهادم اینه که کلشو قرار بدین)
اونها نیاز به کنترلر ندارن بلکه کنترلر هست که نیاز به متغیرهای حالت داره. پس همه متغیرهای حالت رو بیارید
3-حق با شماست. اما باور بفرمایید بعضی وقتا فکر میکنم فیلم داره زیادی طول میکشه. و برای بیننده خسته کننده میشه.
4- متوجه سوالتون نشدم !
درود
ابراهیم
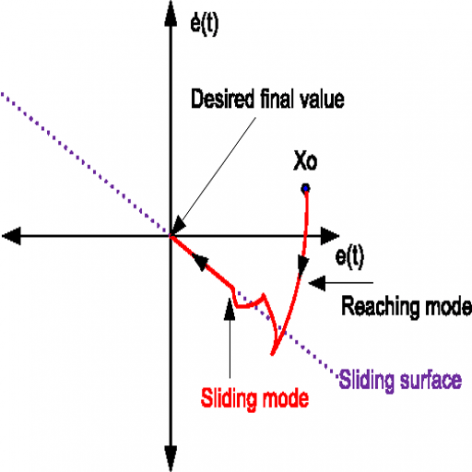
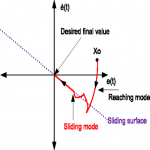
چرا سطح لغزش که بر حسب خطا هستش و در حالت اس مساوی صفر
اما نمودار برحسب متغیرهای حالت رسم میشه(مثل نمودار اول همین صفحه)
مدیر سایتادمین سایت ( مالک تایید شده )
@ابراهیم,
سوالتون خیلی واضح نبود اما فکر کنم منظورتون اینه که چرا توی نموداری که اینجا هستش به جای رسم اس برحسب اس دات متغیرهای حالت رو بر حسب هم رسم کردیم.
دلیلش اینه که توی اون نمودار اس با خود ایکس برابره
ارمین
تدریس به همراه مثال های فراوان و شبیه سازی های مفید
ممنون میشم کنترل مود لغزشی تطبیقی رو هم اضافه کنین
هر روز سایت رو رفرش می کنم تا ببینم کی منتشر میشه
با تشکر
خدا قوت
مدیر سایتادمین سایت ( مالک تایید شده )
@ارمین,
سلام
چشم انشاالله
نظر لطف شماست که به ما محبت دارید
امیرحسین
سلام دکتر
تو کنترل pid با استفاده از خطا ، مشتق خطا و انتگرال خطا کنترلر ایجاد میشه و ورودی مون هم خطاست و واسه تعیین ضرایبش قانون های متفاوتی وجود داره
حالا میشه بفرمایید که مثل تعریف بالا که کنترلر مود لغزشی به صورت کوتاه چیه و ورودیش رو بفرمایید و ضرایبش چه جوری تعیین میشه؟
و واسه من که مکانیکم این آموزش بهتره یا آموزش کوتاه تری که دارین
ممنون
مدیر سایتادمین سایت ( مالک تایید شده )
@امیرحسین,
سلام اقای مهندس
در همه کنترل کننده ها اعم از هوشمند و کلاسیک، ورودی کنترل کننده خطاست ضرایب مد لغزشی هم به صورت های مختلف تعیین میشه.
افراد زیادی از رشته های مکانیک این مجموعه رو خریداری کردن. اگه میخواید پایان نامتون رو انجام بدید حتما این مجموعه رو تهیه و حتی چندین بار نگاه کنید و شبیه سازی ها رو هم خودتون انجام بدین. این سریعترین راه برای یادگیری مد لغزشیه. اگه بخواید کتاب یا مقاله بخونید ماهها درگیر مفاهیم اولیش خواهید شد
درود
امیر حسین
با سلام دوباره و تشکر
میشه چند تا از راه های تعیین ضرایب رو بگید و کدومشون از این روش ها تو این مجموعه تون هستش؟
اگه یه تعریف کوچیک از مد لغزشی بدید ممنونتون میشم؟مثلا جایگاه سطح و چرایی صفر شدنش؟چه جوری به مسئله نگاه می کنه؟ چون یا کتابه سنگینه یا بد توضیح داده؟
این تخفیفتون این هفته چه روز و چه ساعتیه؟چون یک کم قیمت بالاست دکتر منتظرم ها
بی نهایت ممنون
مدیر سایتادمین سایت ( مالک تایید شده )
@امیر حسین,
سلام
همونطوری که برای تعیین پی آی دی روش های زیادی وجود داره اینجا هم روشهای زیادی برای تعیین ضرایب وجود داره
مطمئن ترین راه روش تحلیلیه که قدرت کار شمارو هم بالا می بره. خب این روش به صورت کامل و مفصل توضیح داده شده است.
روش های هوشمند هم یکی دیگه از روشهای تعیین و یا بهبود ضرایب استفاده میشه. ما توی جلسات مد لغزشی فازی به این موضوع پرداختیم.
روشهای عددی مثل الگوریتم ژنتیک، مورچگان، پرندگان، قورباقه ها و تمامی این الگوریتم های جک و جونورها 🙂 قابل استفاده هستن
روشهای تحلیلی دیگه ای هم وجود داره که میشه با اونها ضرایب مد لغزشی رو تعیین کرد یکی از این روش ها کنترل تطبیقیه. این روش به خاطر تحلیلی بودنش از خیلی از روشهای هوشمند و الگورتیم ها بهتر جواب میده
تخفیف از الان اعمال میشه
سپاسگزارم
امیرحسین
سلام
اول ممنون از آموزش خوبتون
تو آموزشتون نمی فرمایید که اصلا تابع علامت چه طور تو معادلات میاد و فقط تاثیراتش رو می گید؟ و از اون مهم تر این که چرا با ueqترکیب شد؟؟ و این که چرا u رو به دو قسمت تقسیم کردید؟
تو جلسه دوم
می گید نامعینی پارامتری با شرط لغزش مقاوم میشه اما در مورد نامعینی غیرپارامتری دیگه اسیر توضیح موضوعات دیگه میشید و دیگه هم توضیح نمیدید
آیا هدف از فیلیپو جواب uدر حالت s=0 است؟
s در اینجا آیا حتما به صورت خطی از خطا باشد؟چون تو بعضی مقالات به صورت دست وپا شکسته من غیرخطی هم دیدم و چرا بعضی اوقات صفحه فاز به صورت منخنی هستش
مدیر سایتادمین سایت ( مالک تایید شده )
@امیرحسین,
سلام
اول تشکر میکنم از نظر خوبتون
ببینید ذات مد لغزشی همون تابع علامته. و این یه روش سر راست برای طراحی یک کنترل کنندست. فلسفش خیلی واضحه . معنی تابع ساین اینه که هر وقت خطا مثبت باشه ورودی منفی و هر وقت خطا منفی باشه ورودی مثبت میشه. اگه روی کاغذ یه سیستم ساده تک ورودی و تک خروجی رو بنویسید با این مفهوم بیشتر آشنا خواهید شد.
اینکه ورودی کنترلی معادل چرا اضافه میشه توی بحث فیلپف توضیح مختصری دادم. بحث ریاضیشو عرض کردم اما یه دلیل قابل لمسش اینه که اگه فقط یک تابع علامت استفاده کنیم و ورودی کنترلی معادل رو استفاده نکنیم ورودی کنترلی زیادی صرف خواهد شد و ورودی کنترلی بین دو عدد از ابتدا تا انتها چترینگ میکنه.
اینکه یو رو به دو قسمت تقسیم میکنم دست ما نیست. این روش مد لغزشیه که میگه ورودی کنترلی دو قسمته یکی پیوسته یکی هم گسسته.
در جلسه دوم نامعینی پارامتری مفصل بحث شده اما ایکاش کل جلسات رو نگاه میکردید چون بحث نامعینی های غیرپارامتری رو در مبحث حذف چترینگ گفتم. چون تا قبل از این نمیشه این مبحث رو مطرح کرد. اینم به خاطر اینه که نامعینی های غیرپارامتری به مبحث چترینگ ارتباط داره.
کلا سه روش برای پاسخ s=0 وجود داره. یکیش فیلپف هست یکیش دینامیک معادل هست و یکیش هم آیزرمن هست که من توی این آموزشها نگفتم چون دیگه واقعا خیلی شلوغ میشد و ضرورتی هم ندیدم و واقعا نه توی پایان نامه نیازه نه توی انجام پروژه . و خیلی ها حتی از اساتید هم این مباحث رو نمیدونن.
سطح لغزش در این آموزش به صورت خطی از خطا هست اما در آموزش انواع مد لغزشی مرتبه بالاتر که توی سایت موجوده سطح لغزش به صورت غیرخطی هم در نظر گرفته میشه (ترمینال اسلایدینگ).
صفحه فاز برای سیستم های با دو متغیر حالت مجموعه ای از خطوط هست اما برای سیستم های با یک متغیر حالت یا مرتبه یک فقط یک منحنی هستش
درود
امیر حسین
دکتر سلام
این آموزشتون خیلی گرونه به نظرم سود کم رو به خرید بیشتر ترجیح بدید بهتره
مدیر سایتادمین سایت ( مالک تایید شده )
@امیر حسین,
سلام
در مقایسه با چیزی که گیر شما میاد خیلی گرون نیست
با این حال اگه واقعا وسع مالی ندارید بهم بگید چقدر تخفیف میخواید
مجید حسین نیا
سلام ممنون از پاسختون
اینطور که فرمودید ورودی کنترلی u1 برحسب دوتا سطح لغزش s1 و s2 به دست میاد ؟
یعنی در شبیه سازی u1 دوتا تابع sign میاد درسته ؟
مدیر سایتادمین سایت ( مالک تایید شده )
@مجید حسین نیا,
سلام خواهش می کنم
برای سیستم شما بله
مجید حسین نیا
سلام آقای دکتر وقتتون به خیر
برای سیستم زیر میخوام کنترل کننده مد لغزشی طراحی کنم اما موندم توش
خیلی لطف میکنید اگه کمکم کنید
xdot2= a2* x1 + b2*x2 -x3*u2
(xdot3 = a3( u1*x1 + u2*x2
برای x2 و x3 میخوام کنترل کننده کننده طراحی کنم توی رابطه دوم دوتا ورودی هست.ueq و u نهایی رو چگونه میشه به دست آورد ؟
ممنون از لطفتون
مدیر سایتادمین سایت ( مالک تایید شده )
@مجید حسین نیا,
سلام وقت بخیر
ممنون از سوال خوبتون.
همونطور که توی جلسه هشتم عرض کردم سیستم هایی از این دست خیلی نادر هستن که ضریب ورودی کنترلی یک ماتریس غیرقطری باشه. اما در مورد سیستم شما طراحی براساس مطالبی که توی فیلم های آموزشی عرض کردم براحتی قابل انجامه.
الگوریتم طراحی:
یک. سطح لغزش اول رو بصورت زیر در نظر بگیرید
s1=x2-x2d
و براساس گفت های فیلم های آموزشی پیش برید و ورودی کنترلی دوم رو بدست بیارید.(حالتی حدبهره نامعینی ندارد)
دو.ورودی کنترلی دوم رو که از مرحله اول بدست آوردید در معادلات دوم جایگذاری کنید حالا معادلات شما فقط یک ورودی دارند و میتونید مد لغزشی رو برای ورودی اول هم بدست بیارید.(حالتی که حد بهره نامعینی دارد)
در مرحله دوم سطح لغزش رو به صورت زیر باید در نظر بگیرید
s2=x1-x1d
درود
عادل
سلام
آقای دکتر از پاسخ سریع شما بسیار ممنون. اقای دکتر درخصوص مینیمم فاز بودن مطمئن هستید؟
من در مواجهه با سیستم تحت مطالعه خودم ، چند مشکل دارم:
۱- مقدار u2 بایستی بین ۰٫۵- , ۰٫۵+ باشه و مقدار u1 باید بین ۰٫۵ تا یک باشه . اگر اشباع در خروجی کنترل کننده لغزشی قرار دهم چه مشکلی پیش می آید؟ ایا این محدود سازی کنترل کننده نیست؟
۲- هدف اصلی ردیابی x2 و x3 است البته چون من کار عملی انجام می دهم نمی خواهم x1 از یک حدی بیشتر شود درضمن عملا x1 و x2 نمی توانند هرگز منفی شوند.چگونه این قیود را در کنترل کننده لحاظ کنم؟
و سوال آخر اینکه درصورتیکه از PWM برای اعمال کنترل کننده به سیستم اصلی استفاده کنیم عملا فرکانس u ها به فرکانس PWM محدود می شود. در واقع در این شرایط چترینگ چگونه خواهد بود؟ ایا باز چترینگ معنی دارد؟
از اینکه وقت گذاشته و پاسخ می دهید بسیار ممنون.
با تشکر فراوان
مدیر سایتادمین سایت ( مالک تایید شده )
@عادل,
سلام مجدد
در مورد مینیمم فاز بودن در روش پسگام که توی کتاب اسلاتین به صراحت گفته که این روش برای سیستم های مینمم فاز و غیرمینمم فاز هستش برای مد لغزشی هم من تا به الان ندیدم که بحث غیرمینمم فاز بودن بررسی بشه. چون این روشها براساس تابع لیاپانوف هستن به نظرم اهمیتی نداره که سیستم مینمم فاز باشه یا نه.
۱- ظاهرا سیستم شما دارای اشباع روی ورودی هستش بنابراین باید به سراغ روشهایی برید که اشباع رو هم در نظر میگیرند. اما ساده ترین کاری که میتونید انجام بدید اینه که کنترل کننده رو طراحی کنید و بعد اشباع روی ورودی بگذارید این اشباع معمولا نمیتونه بیشتر از ده بیست درصد کاهش پیدا کنه . یعنی مثلا اگه دامنه وردی شما ده باشه دیگه تا نیم نمیتونه پایین بیاد و حداکثر تا هشت یا هفت بتونید روش اشباع قرار بدید. این یک روش مرسومه.
اگه اشباع رو از یک حد بیشتر کنید سیستم ناپایدار خواهد شد.
۲- اینکه متغیرهای حالتتون هم نمیتونن از یک حد بیشتر باشند قاعدتا باید در بطن معادلات حالتتون این قیود وجود داشته باشن و اگه وجود ندارن احتمالا معادلات حالت کاملی در اختیار ندارید. اما برای رفع این مشکل شما باید یک تابع هزینه تعریف کنید که این قیود رو هم شامل بشه. مگه اینکه با ضرایب کنترل کننده ساده مد لغزشی اینقدر بازی کنید تا حالت هاتون از مقادیری که فرمودید تجاوز نکنن.
در مورد سوال آخرتون اگه ورودی کنترلی نهایتا همونطوری که طراحی میشه به سیستمتون اعمال نشه قاعدتا نباید مدهای فرکانس بالای سیستمتون رو که مدل نشدن تحریک کنه. اما من در این مورد خیلی اطلاعاتی ندارم.
مدیر سایتادمین سایت ( مالک تایید شده )
@مدیر سایت,
سلام دکتر
ظاهرا حق با شماست. یک نفر سیستمی به من داد که در اون نیاز به بررسی پایداری دینامیک داخلی داشت.
برای بررسی دینامیک داخلی دقیقا مثل روش خطی سازی با فیدبک باید عمل کرد
عادل
سلام
اقای دکتر بنده فیلم های آموزشی شما را مشاهده نمودم و برای اینجانب بسیار مفید بود. درصورت امکان لطفا به سوالات اینجانب پاسخ دهید. درصورتیکه سیستم غیر حداقل فاز باشد چه ملاحظاتی در استفاده از کنترل کننده مد لغزشی لازم است به عمل آید.در برخی از مقالات استفاده از یک PI را در ترکیب با SMC پیشنهاد کرده اند (روش کنترل دوحلقه ای با غیر مستقیم) که البته به نظر اینجانب وجود PI مزایای SMC را زیر سوال می برد.
درضمن درصورتیکه در مثال جلسه ۸ اگر هر دو ورودی کنترلی در یک متغیر حالت ظاهر گردد مثلا به فرم زیر باشد انگاه روند طراحی به چه صورت خواهد بود.
x1d=a1*x1^2*x2-b1*(x4^2+1)*u1+b2*u2;
با تشکر
مدیر سایتادمین سایت ( مالک تایید شده )
@عادل,
عرض سلام و احترام
ممنون ازینکه سوالتون رو توی سایت مطرح فرمودید
اما در مورد مینیمم فاز نبودن. در روش های مد لغزشی و بک استپینگ اهمیتی نداره که سیستم مینمم فاز باشه یا نباشه . این قضیه در روش خطی سازی با فیدبک اهمیت پیدا میکنه. اما در روش مد لغزشی برای ما اهمیت نداره که سیستم غیرمینیمم فاز هست یا نه.
در مورد سیستمی که مثال زدید من توی اون جلسه عرض کردم که اینطور سیستمها خیلی نادر هستن ولی اگه واقعا سیستمون به این فرم باشه باید براساس کتاب پیش برید و مهمترین قسمت طراحیش تخمین ماتریس بی هستش.
بقیش کار پیچیده ای نیست.