احتمالا برای شما هم پیش اومده که در یک مقاله یا کتاب به جایی رسیدید که باید یک ناتساوی ماتریسی خطی (یا LMI) رو حل کنید و در بدر دنبال یک نفر هستید تا در کوتاهترین زمان ممکن حل این نوع ناتساوی ها رو به شما یاد بده تا مجبور نباشید زمان قابل توجهی صرف کنید و از منابع مختلف دنبال راه حل باشید. اگر شما هم جزو این دسته از محققین هستید دیگه نگران نباشید. در این پست قراره تمام جزییات و کلیات نامساوی ماتریسی خطی (و حتی غیرخطی) با نحوه حل اونها در متلب و با دو روش تولباکس متلب و YALMIP به روش ساده و با مثالهای مفصل توضیح داده بشه. اگر با این فیلمهای آموزشی همراه شده و مرحله به مرحله مثالها رو پیش برید بعد از این 11 جلسه قادر خواهید بود حل کننده (solver) مناسب رو برای مساله خودتون انتخاب کرده و ناتساویهای ماتریسی خودتون رو باهاش حل بکنید. بعد از تشریح کامل دو روش بالا یک مثال از طراحی کنترل کننده برای سیستم شناور مغناطیسی از یک مقاله IEEE با استفاده از LMI خدمت شما ارایه میشه (به همراه شبیه سازی در محیط سیمولینک) تا مطلب کامل جا بیافته. با ما همراه باشید…
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری سیستمهای کنترل خطی – آشنایی با کدنویسی در محیط متلب
جلسه اول: مقدمات ریاضی و تعریف ناتساوی های ماتریسی
در این جلسه ابتدا مقدمات ریاضی و تعریف ناتساوی های ماتریسی به همراه مفاهیم مجموعه های محدب و نامحدب توضیح داده میشه و چند مثال هم از هر دو نوع مجموعه ارایه میشود. سپس نحوه تبدیل ناتساویهای خام به حالت استاندارد تشریح شده و در انتها روشهای مختلف حل عددی ناتساویهای ماتریسی به طور خلاصه مطرح میشود. جهت ارزیابی شما عزیزان جلسه اول رایگان تقدیم میشود.
مدت زمان آموزش: 49 دقیقه
محتویات درس: فیلم با کیفیت 720p و پاورپوینت درس
حجم فایل: 65 مگابایت
پیش نمایش جلسه اول:
جلسه دوم: تعیین متغیرهای ماتریسی و وارد کردن جملات LMI در تولباکس متلب
در این جلسه کار با تولباکس LMI متلب را شروع کرده و مراحل مختلف ایجاد یک LMI ارایه میشود. به طور خاص نحوه تعیین متغیرهای ماتریسی و همینطور نحوه وارد کردن جملات داخلی و خارجی به همراه مثال در محیط متلب تشریح میشود.
مدت زمان آموزش: 69 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس- کد متلب مربوط به مثالها- فایل pdf راهنمای استفاده از تولباکس متلب و لیست مرتب شده تمام دستورات مرتبط با تولباکس LMI متلب
حجم فایل: 89 مگابایت
پیش نمایش جلسه دوم:
جلسه سوم: معرفی دستور feasp تولباکس متلب جهت حل LMI
در این جلسه دستورات مختلفی که برای کسب اطلاعات تکمیلی از متغیرها و LMI های تعریف شده در متلب وجود دارند بررسی شده و با مثال تشریح می شوند. در ادامه یکی از دستورات مهم تولباکس LMI متلب که برای حل مسایل ناتساوی مورد استفاده قرار میگیرد معرفی شده و یک مثال از تحلیل پایداری سیستم کنترلی برای آن ارایه میشود.
مدت زمان آموزش: 68 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 100 مگابایت
پیش نمایش جلسه سوم:
جلسه چهارم: معرفی دستورات mincx و gevp تولباکس متلب جهت حل مسایل مینیممسازی
در این جلسه ابتدا دستور mincx که برای حل ناتساویهای ماتریسی با شرط مینیمم سازی (یا ماکزیمم سازی) استفاده میشود به طور کامل تشریح شده و مثال جلسه قبل با شرط مینیمم و ماکزیمم سازی دوباره با این دستور حل میشود. همچنین دستور gevp که مربوط به حل مسایل مینیمم سازی مقدار ویژه تعمیم یافته میباشد تشریح میشود.
مدت زمان آموزش: 51 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 69 مگابایت
پیش نمایش جلسه چهارم:
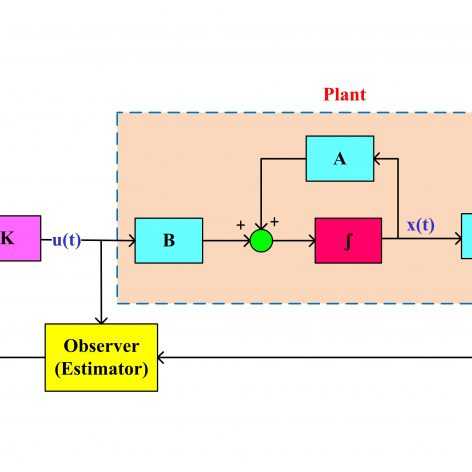
جلسه پنجم: طراحی کنترل کننده فیدبک حالت برای سیستم خطی و حل LMI های آن با تولباکس متلب
در این جلسه ابتدا دستورات باقیمانده که مربوط به ارزیابی LMI بعد از حل آن است معرفی میشوند. در ادامه یک مثال از طراحی کنترل کننده فیدبک حالت برای سیستم خطی به شکل LMI فرمول بندی شده و با تولباکس LMI متلب حل میگردد. نهایتا دو ترفند بسیار پرکاربرد تبدیل متجانس (Congruent transformation) و لم شور (Schur complement) برای LMI بیان میشوند.
مدت زمان آموزش: 53 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 76 مگابایت
پیش نمایش جلسه پنجم:
جلسه ششم: معرفی تولباکس یالمیپ برای حل LMI و نجوه دانلود و نصب آن
از این جلسه معرفی تولباکس YALMIP شروع میشود و ابتدا توضیحات مقدماتی درباره آن و مزایای آن نسبت به تولباکس متلب ارایه میشود. در ادامه تمامی مراحل دانلود و نصب این تولباکس بر روی متلب به صورت گام به گام تشریح میشود. در انتها نحوه ارزیابی نصب درست تولباکس و solver های موجود در آن توضیح داده میشود.
توجه: اخیرا ظاهر و پوسته سایت YALMIP دچار تغییر و تحول شده و با صفحات نشان داده شده در فیلمهای حاضر قدری متفاوت است. با توجه به اینکه محتویات سایت YALMIP تغییر پیدا نکرده و تنها محل لینکها تغییر پیدا کرده (مثلا لینکهای ستونی سمت چپ به بالای صفحه انتقال پیدا کرده)، فیلمهای موجود دوباره ضبط نشده و همین فیلمها قابل استفاده هستند.
مدت زمان آموزش: 47 دقیقه
محتویات درس: فیلم آموزشی
حجم فایل: 96 مگابایت
پیش نمایش جلسه ششم:
جلسه هفتم: تعریف متغیرهای ماتریسی و قیدها با استفاده از تولباکس یالمیپ
در این جلسه ابتدا نحوه تعریف متغیرهای ماتریسی با مثالهای متنوع در محیط متلب توضیح داده شده و سپس چگونگی تعریف قیدها یا همان ناتساویهای ماتریسی جهت استفاده در YALMIP با چندین مثال تشریح میشود.
مدت زمان آموزش: 62 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 85 مگابایت
پیش نمایش جلسه هفتم:
جلسه هشتم: تعریف تابع هزینه و حل LMI با استفاده از تولباکس یالمیپ
در این جلسه نحوه تعریف تابع هزینه، گزینه های اختیاری مربوط به YALMIP (به جز solver ها)، چگونگی حل مساله و در نهایت روش استخراج متغیرهای ماتریسی تشریح شده و مثال تحلیل پایداری که جلسات پیش با تولباکس متلب حل شده بود، با YALMIP هم حل میشود.
مدت زمان آموزش: 71 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 114 مگابایت
پیش نمایش جلسه هشتم:
جلسه نهم: معرفی و تشریح نحوه دانلود و نصب سه solver پرکاربرد به نامهای PENBMI ، SDPT3 و MOSEK
مباحث باقیمانده از توضیحات مربوط به YALMIP از جمله solver ها (داخلی و خارجی) در این جلسه مورد بحث قرار میگیرد. به طور خاص نحوه دانلود و نصب سه solver پرکاربرد به نامهای PENBMI ، SDPT3 و MOSEK به طور کامل تشریح شده و مثال تحلیل پایداری سیستم خطی که در جلسات قبل با تولباکس متلب حل شده بود، با این سه solver نیز حل میگردند.
مدت زمان آموزش: 73 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 169 مگابایت
پیش نمایش جلسه نهم:
جلسه دهم: معرفی دینامیک غیرخطی قطار مغناطیسی شناور و خطیسازی حول نقطه کار
در این جلسه تکنولوژیهای موجود در ساخت قطارهای مغناطیسی معرفی شده و دینامیک غیرخطی شناورسازی یک قطار مغناطیسی با تکنولوژی EMS از یک مقاله IEEE ارایه میشود. در ادامه نقاط تعادل و نامی دینامیک استخراج شده و حول نقطه مورد نظر خطیسازی ژاکوبی انجام میشود تا ماتریسهای مورد نیاز برای طراحی کنترلکننده فیدبک حالت بدست آورده شود.
مدت زمان آموزش: 66 دقیقه
محتویات درس: فیلم آموزشی و کلیپی کوتاه از عملکرد قطار مغناطیسی- فایل پاورپوینت و مقاله IEEE حاوی دینامیک شناورسازی قطار مغناطیسی
حجم فایل: 116 مگابایت
پیش نمایش جلسه دهم:
جلسه یازدهم: طراحی و شبیهسازی فیدبک حالت برای سیستم شناور مغناطیسی
در این جلسه ابتدا دینامیک غیرخطی شناور مغناطیسی در محیط متلب و در نقطه کار دلخواه خطی شده و سپس با هر دو روش تولباکس LMI متلب و YALMIP مساله پایدارسازی سیستم خطی شده با فیدبک حالت حل میشود. همچنین بعد از بدست آوردن بهره کنترل کننده با استفاده از solver های PENBMI، SDPT3 و MOSEK در محیط YALMIP و بهره بدست آمده از تولباکس متلب، سیستم حلقه بسته (با دینامیک غیرخطی) در محیط سیمولینک شبیه سازی شده و نتایج حاصل از این بهره ها باهم مقایسه شده است.
مدت زمان آموزش: 67 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کدها و فایلهای شبیه سازی سیستم حلقه بسته
حجم فایل: 113 مگابایت
پیش نمایش جلسه یازدهم:
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم


بابک
سلام
معادله همیلتون ژاکوبی غیر خطی رو میشه با یالمیپ به صورت عددی حل کرد؟
برای پیدا کردن فیدبک حالت بهینه
مدیر سایتادمین سایت ( مالک تایید شده )
@بابک,
سلام
در حالت کلی هر نامساوی ماتریسی غیرخطی رو نمیشه با YALMIP حل کرد مخصوصا اگه غیر محدب باشه. اگر بتونید معادله همیلتون ژاکوبی رو به BMI تبدیل کنید با استفاده از solver خوب PENBMI میتونید حلش کنید اما اگه BMI نباشه (و غیرخطی مرتبه بالا باشه)، solver مناسبی برای حلش وجود نداره و اونهایی که موجود هستند خیلی کارایی ندارند مثل BMIBNB
نازنین
با سلام
در مورد مقاله زیر که کنترل پیش بین سیستمهای متصل به هم با قید QDC می باشد ، تابع هزینه J را باید در حضور قید QDC آورده شده در ناتساوی شماره 7 که این قید به صورت BMI می باشد حل کنیم. اما با این مشکل مواجه شدیم که باید با کدام solver در Yalmip حل شود؟
https://pdfs.semanticscholar.org/dbf1/0b9183b76bc265275c2181f1a6b3f5eff462.pdf
مدیر سایتادمین سایت ( مالک تایید شده )
@نازنین,
با سلام و عرض معذرت به خاطر تاخیر در پاسخ دهی.
همونطور که در جلسه نهم توضیح دادم، برای حل BMI میشه از solver خوب PENBMI استفاده کرد. البته این solver پولی بوده و باید خریداری بشه اما عملکردش قابل قبوله
رضا
با سلام
یک سوال در مورد سالور Mosek داشتم. اگر این سالور از طریق ایمیل دانشگاهی و بصورت academic دانلود بشه، آیا محدودیت نصب روی چند سیستم رو داره؟ در واقع سوالم اینه ایا از یک لایسنس گرفته شده میشه بروی چند سیستم استفاده کرد؟
علی جوادی
@رضا,
سلام
فقط روی یک سیستم قابل استفاده است
امیر کاظمی
با سلام و احترام،
صفحه 11 مقاله ای که در آخر پست لینکش رو قرار دادم، یک مسئله LMI را با روش differential evolution حل کرده است. میتونید در این مورد کمی توضیح دهید؟ آیا در آموزش هایی که گذاشته شده از این روش هم استفاده شده است؟ تولباکس متلب از این روش پشتیبانی می کند و اگر نمی کند باید از چه نرم افزار یا تولباکسی استفاده کرد؟
با تشکر.
http://www.sciencedirect.com/science/article/pii/S001600321500410X
علی جوادی
@امیر کاظمی,
با سلام
این روش برای حل مسایل غیر محدب (در این مقاله دوخطی) استفاده میشه و یک روش فرا ابتکاریه. من در آموزشها فقط solver ها رو معرفی کردم و نحوه حل مساله توسط اونها رو توضیح ندادم. بنابراین در مورد این روش هم توضیحی ندادم. مهم اینه که شما از یک solver که مساله شما رو حل میکنه بتونید استفاده کنید (مثلا از طریق YALMIP).
البته اگر علاقمند به پیادهسازی یک روش خاص مثل DE باشید، میتونید از الگوریتم ارائه شده در فلوچارت شکل 2 استفاده کرده و با استفاده از هر تولباکسی که LMI حل میکنه (تولباکس متلب یا YALMIP) این روش رو پیادهسازی کنید. در واقع با این روش مساله غیر محدب تبدیل به حل چند LMI میشه و در این مقاله اون LMI هارو با تولباکس متلب حل کرده.
همونطور که تو فیلمها گفتم، برای حل نامساویهای دو خطی میتونید داخل YALMIP از solver PENBMI استفاده کنید که عملکرد خوبی داره ولی پولیه.
امیدوارم توضیحات کافی باشه
امیر کاظمی
@علی جوادی,
بسیار مفید بود، سپاس.
علی
ممنون از راهنمایی خوب شما
علی
سلام ممنون از راهنماییتون
از حل LMIهم که بگذریم و مقادیر P,L,B را معلوم فرض کنیم و K را از رابطه ذکر شده بدست اوریم رابطه ی L=PBK را برقرار نمیکند. ولی اثبات رابطه ذکر شده ظاهرا درست است.
برای اثبات داریم : چون P معکوس پذیر است بنابراین با ضرب از سمت چپ طرفین رابطه ی L=PBK در P^-1 خواهیم داشت:BK=P^-1*L .با ضرب دو طرف تساوی از چپ در ماتریس B’ خواهیم داشت:B’*B*K=B’*P^-1*Lو چون B’*B معکوس پذیر است بنابراین با ضرب دو طرف مساوی از چپ در معکوس B’*B خواهیم داشت
K=(B’*B)^-1*B’*P^-1*L ولی K بدست امده رابطه L=PBK را براورده نمیکند.به این رابطه خیلی نیاز دارم ممنونم اگر راهنمایی کنید.
لینک مقالهhttp://www.sciencedirect.com/science/article/pii/S0016003214003573
علی جوادی
@علی,
سلام
صفحه دوم مقاله اگر دقت کنید (پاراگراف سوم از آخر) توضیح داده که از روش best scalars selection استفاده کرده و اعتراف کرده که نمیشه جواب دقیق بدست آورد و بنابراین بهترین K که ماتریسهای L و PBK رو به هم نزدیک کنه، بدست آورده. همه اینا هم به خاطر این بوده که نتونسته مساله رو به فرم LMI در بیاره و برای تبدیل مساله از حالت quasi-convex به convex از این ترفند نادرست استفاده کرده. با این که ژورنال خوبیه ولی این مقاله متاسفانه سطح پایینی داره تضمینی برای پایداری سیستم با این روش وجود نداره حتی اگه شبیه سازی هم جواب بده. حتی مقادیر PBK و L مثال حل شده داخل خود مقاله هم برابر نیست!!! به شما هم توصیه میکنم از این روش استفاده نکنید
موفق باشید
علی
سلام
در حالت عادی نمیشه ولی ایا مراحل زیر می تواند درست باشد؟
pوL توسط متلب بدست می آید و pیک ماتریس2*2 است و B یک ماتریس 1*2 و L یک ماتریس 2*2 است و گین Kنیز باید 2*1 باشد. بنابراین می توان گین K را از رابطه ی زیر بدست آورد(این راه حل یکی از مقالات ژورنال است):
K=(B’B)^-1*B’*P^-1*L
علی جوادی
@علی,
سلام
خواهش من اینه که دوباره جواب قبلی من رو با دقت خیلی بیشتر بخونید. ولی برای اینکه مساله کاملا مشخص بشه من یک مثال نقض برای این راه حلی که شما پیدا کردید ارائه میکنم.
فرض کنید [2- 1- ;1 0]=A و [1;0]=B باشند. کد زیر برای شما مقادیر P مثبت معین و L رو محاسبه می کنه:
clear all;close all;clc
A=[0 1;-1 -2];B=[0;1];
P=sdpvar(2,2);L=sdpvar(2,2);
C=[ A’*P+P*A+L+L’=0 ];
optimize(C);
Pv=value(P)
Lv=value(L)
K=(B’*B)\B’/Pv*Lv
مقادیر بدست اومده به شکل زیر هستند:
P=[1 0;0 1]
L=[-0.5 0;0 1.5]
K=[1.5 0]
حالا اگه PBK رو با مقادیر بدست اومده محاسبه کنید داریم:
[1.5 0;0 0]=PBK
در حالی که L برابر این مقدار نیست!
علتش هم همون چیزیه که تو جواب قبلی خدمتتون عرض کردم. البته با توجه به اینکه ‘ (B’*B)\B معکوس مجازی B هستش، بنابراین از این رابطه که گفتید مقدار K طوری بدست میاد که فاصله بین نرم ماتریسهای L و PBK مینیمم بشه و همونطور که میبینید ماتریس L و PBK تو این مثال فقط تو یه درایه باهم فرق دارند و بقیه مقادیرشون یکسانه. ولی در حالت کلی به دلایلی که قبلا گفتم نمیشه هیچ جواب دقیقی بدست آورد.
لطفا لینک اون مقاله رو همینجا بفرستید تا ببینم که آیا ژورنال معتبری هست یا نه؟
با درود
علی
سلام وقت بخیر
ایا ممکن است در حل نامساوی ماتریسی مثلا عبارت PBK که PوK مجهول و B معلو م است ، تغییر متغییر L=PBK را انجام داد و آن را حل کرد؟
ممنون میشم اگه جواب بدین.
علی جوادی
@علی,
با سلام و تشکر از سوال خوبی که پرسیدید.
احتمالا منظور شما از این سوال این بوده که برای طراحی کنترل کننده فیدبک حالت که باید LMI زیر حل بشه، میشه این تغییر متغیر رو داد یا نه؟ (چون بعیده تو یه مساله کنترلی فقط جمله PBK به تنهایی ظاهر بشه که در اینصورت تغییر متغیر امکان پذیره ولی به دردی نمیخوره چون در عمل این حالت پیش نمیاد!)
A’P+PA+PBK+K’B’P<0
در اینصورت جواب شما منفیه به خاطر اینکه اگر این تغییر متغیر رو بدید، باید P موجود در جملات A'P و PA رو هم بر حسب متغیر جدید بنویسید یا رابطه اونا رو با L تعیین کنید. اگه قرار باشه L یه ماتریس جدید باشه و P هم یه ماتریس جدا باشه که باید توسط متلب پیدا بشه، اونوقت دیگه رابطه بین P و K با L از بین میره و شما نمیدونید به ازای اون P و L داده شده آیا میشه یک K پیدا کرد که رابطه L=PBK برقرار باشه یا نه؟ برای روشن شدن بحث فرض کنید P یک ماتریس متقارن دو در دو، B یک ماتریس دو در یک، K یک ماتریس یک در دو باشند و بنابراین L یک ماتریس دو در دو خواهد بود. حالا اگه P و L به صورت مستقل توسط متلب پیدا بشه (با حل A'P+PA+L+L'<0) و شما مقدارشونو بدونید، از مساوی قرار دادن L و PBK چهار معادله دارید در حالی که فقط دو متغیر داخل K دارید که باید طوری تعیین بشوند که همه چهار معادله برقرار باشه که در حالت کلی غیر ممکنه. اگه رو کاغذ یکبار بنویسید کاملا مطلب جا میافته.
درود
ali
سلام. اگر می شود لطفا PENBMI را برای دانلود قرار دهید.
علی جوادی
@ali, با سلام. دوست عزیز همانطور که داخل فیلمها هم اشاره کردم، PENBMI یک solver رایگان نیست و باید برای استفاده از آن خریداری شود.
درود
ali
@علی جوادی,
یعنی شما هم آن را ندارید؟
علی جوادی
@ali, نسخهای که من دارم صرفا برای مصارف تحقیقاتی بوده و برای دانشگاه علم و صنعت ایران خریداری شده و فقط دانشجویان این دانشگاه اجازه استفاده از اون رو دارند و من اجازه ندارم اونو در اختیار عموم قرار بدم. هر فرد یا دانشگاهی که نیاز داشته باشه باید اون رو خریداری کنه. البته توصیه میکنم نسخه آکادمیکش رو از طریق دانشگاهتون تهیه کنید که ارزونتره.
اجازه بدید یه توصیه کلیتر هم بکنم. همیشه سعی کنید مساله رو طوری فرمولبندی کنید که به LMI برسید و بنابراین نیازی به solver هایی مثل PENBMI نداشته باشید. این کار دو مزیت داره:
1) نیازی به هزینه کردن برای خرید PENBMI نیست.
2) معمولا دید خوبی نسبت به مسایل غیرمحدب در بین داوران ژورنالهای معتبر وجود نداره و بنابراین اگر مقالهای نگارش کنید که باید توش یه شرط BMI حل بشه احتمال رد شدن مقاله وجود داره.
موفق باشید
ali
@علی جوادی,
ممنون که جواب دادید.
قید من quasi-convex است.
بازم اگه لطف کنید برام ایمیل کنید ممنون میشم ازتون.
علی جوادی
@ali, متاسفانه امکانش نیست که این solver رو در اختیار هیچ کسی بذارم ولی قطعا میتونید الگوریتم های تکراری رایگان پیدا کنید که مسایل quasi-convex رو براتون حل بکنه.
موفق باشید
یاسمن
سلام
وقت بخیر
آقای دکتر آیا دستور mincx فقط برای حالت مینیم سازی بصورت cx قابل استفاده است؟
مثلا اگر یک پارامتر را (نه یک تابع) را بخواهیم مینیمم کنیم چطور؟
مثلا قرار است نامساوی ماتریسی حل شود به شرط مینیمم سازی پارامتر d. که در ماتریس هم، پارامتر d بصورت ضرب در ماتریس واحد روی قطرهای اصلی قرار دارد. مثلا سطر اول به این صورت است…
[dI BP-GC] (متاسفانه امکان اتچ کردن تصویر وجود ندارد و امکانات ویرایش هم در این صفحه محدود می باشد)
G,P هم ماتریس های نامعلوم هستند که با حل LMI بدست می آیند.
جناب دکتر جوادی قبلا از پاسخگویی شما سپاسگزارم
علی جوادی
@یاسمن, با سلام
اولا که تمام مجهولات شما چه ماتریسی، چه برداری و چه اسکالر همگی جزو متغیرهای LMI هستند و همگی داخل بردار تصمیم گیری یا x قرار دارند و شما با دستور mincx میتونید هر ترکیب خطی از این متغیرها رو (که همون cx باشه) مینیمم کنید. تنها کاری که شما باید بکنید اینه که محل اون متغیر دلخواه رو تو بردار تصمیم گیری پیدا کنید تا بردار c رو تعیین کنید (مثلا ضریب متناسب با اون متغیر تصمیم گیری رو تو بردار c یک کنید و بقیه رو صفر کنید). روشهای مختلفی برای این کار وجود داره که تو جلسه چهارم (تقریبا دقایق 4 تا 12) با یک مثال کاربردی مفصلا بحث شده. در واقع یکی از روشها دستور defcx هستش که تو فیلم به طور کامل توضیح داده شده.
موفق باشید
یاسمن
فراااااوااااان سپاااااااااس 🙂
حل شد فقط دقتش مناسب نیست.
علی جوادی
@یاسمن, برای بهتر شدن دقت شاید بهتر باشه از تولباکس YALMIP با solver MOSEK استفاده کنید.
درود