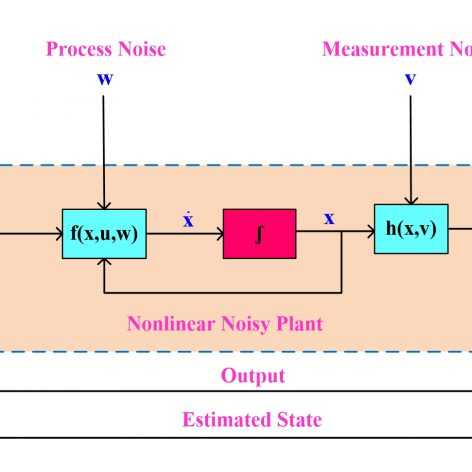
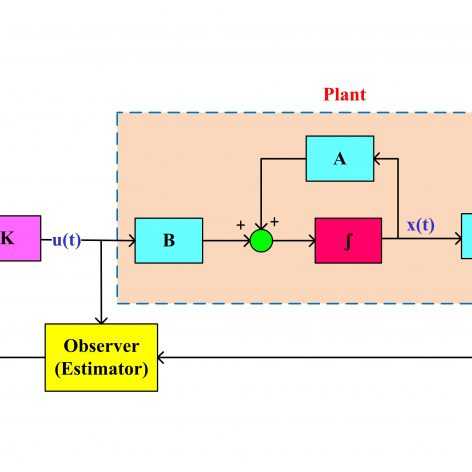
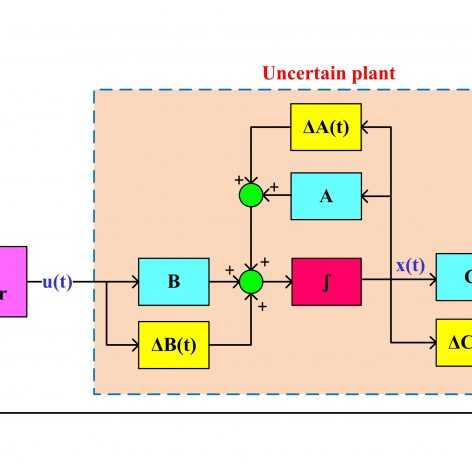
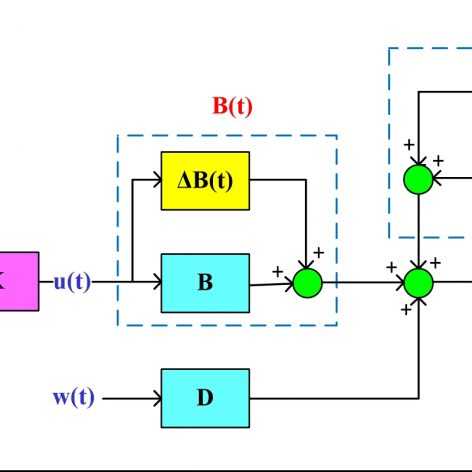
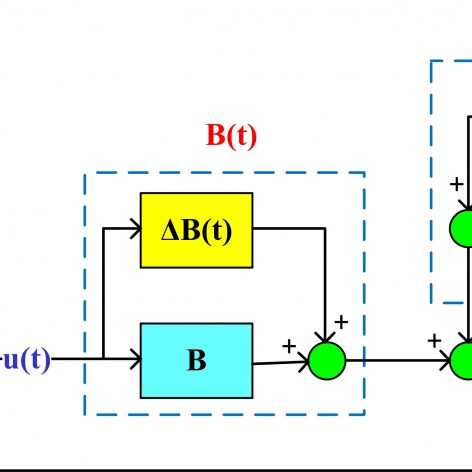
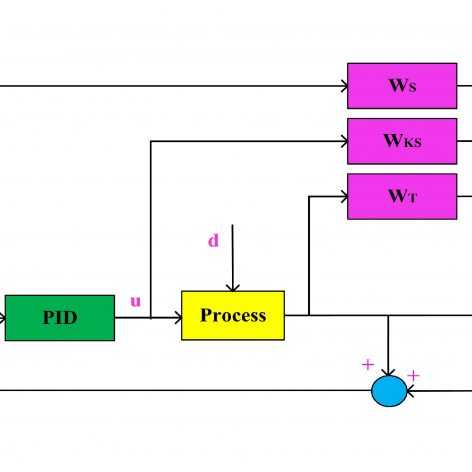
فیلمهای مربوط به کنترل مقاوم فیدبک حالت سیستمهای خطی تحت اغتشاش و همچنین کنترل فیدبک خروجی سیستمهای خطی با استفاده از رویتگر قبلا خدمت دوستان تقدیم شده است. اگر سیستمی هم تحت تاثیر اغتشاش خارجی بوده و هم امکان اندازهگیری تمامی حالتها وجود نداشته باشد، دیگر نمیتوان از این فیلمها برای چنین سیستمی استفاده کرد. در سری فیلمهای حاضر دقیقا این مشکل مدنظر قرار گرفته و هدف طراحی یک کنترلکننده مقاوم برای سیستمهای خطی تحت تاثیر اغتشاش فقط با استفاده از یک یا چند خروجی سیستم است. کنترل کننده مورد نظر دارای رویتگر نبوده ولی دارای دینامیک داخلی است. همچنین تنها از خروجی سیستم فیدبک گرفته شده و نیازی به ورودی سیستم تحت کنترل ندارد. معیار تضعیف اغتشاش همان نرم ∞H است که به تفصیل در سری فیلمهای کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی تشریح شده و ارتباط آن با تلف کنندگی (Dissipativity) و پایداری بهره L2 بحث شده است. برای اطلاعات بیشتر در مورد تضعیف اغتشاش از طریق نرم ∞H و مزایای فرمولبندی این مساله به شکل LMI به فیلمهای مربوط به کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی مراجعه کنید.
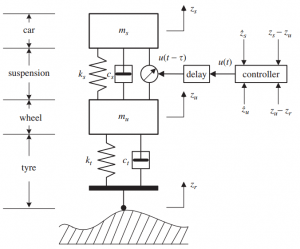
بعد از محاسبه نامساویهای ماتریسی خطی لازم برای حل مساله که ایده اصلی آن از یک مقاله IEEE گرفته شده است، روش پیشنهادی بر روی یک مدل یک چهارم سیستم تعلیق خودرو پیاده شده و سیستم حلقه بسته هم در محیط m-file و هم در سیمولینک شبیهسازی شده است. همچنین توابع تبدیل از نویز اندازه گیری، اغتشاش خارجی و ورودی مرجع به خروجی محاسبه شده و پهنای باند سیستم حلقه بسته و خواص تضعیف نویز و اغتشاش به صورت تحلیلی و شبیهسازی مورد بررسی قرار گرفته است. لازم به ذکر است که سیستم تعلیق در این سری فیلمها فقط به عنوان یک مثال کاربردی مورد استفاده قرار گرفته است و توضیح اضافی در مورد آن ارائه نشده است. برای درک بهتر این مثال شاید بهتر باشد قبل از دیدن این سری فیلمها، جلسات مربوط به مدلسازی و شبیهسازی ارتعاشات جاده برای سیستم کنترل تعلیق فعال خودرو را ملاحظه کنید و بعد از اینکه با سیستم تعلیق آشنا شدید، این سری فیلمها را ببینید.
با امید به اینکه مورد رضایت شما عزیزان قرار بگیرد
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
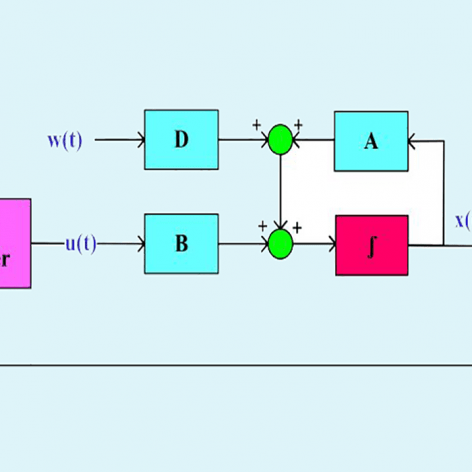
فرمولبندی طراحی کنترل مقاوم فیدبک خروجی برای سیستمهای دارای اغتشاش خارجی
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
پیادهسازی کنترلکننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیهسازی در متلب
شبیهسازی در محیط سیمولینک و تحلیل در حوزه فرکانس
جلسه دوم:
جلسه سوم:
جلسه چهارم:
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



غلامرضا بامی محمدی
من برای مدل کامل سیستم تعلیق ماتریس های فضای حالتو استخراج کردم ولی lmi feasible نمیشه. گاما هم تغییر میدم. آیا برای گاما مرز خاصی تعریف میشه یا میشه هر مقداری بگیره؟
علی جوادی
@غلامرضا بامی محمدی,
سلام
اصولا گاما ابتدا یه مقدار بزرگ انتخاب میشه اونقدر که LMI حل بشه. بعد گاما رو کمتر میکنیم تا جایی که همچنان LMI قابل حل باشه. هر چقدر گاما کوچکتر انتخاب بشه تضعیف اغتشاش بیشتره.
سعی کنید گاما رو تا جایی بیشتر کنید تا LMI حل بشه
غلامرضا بامی محمدی
با سلام تشکر فراروان از آموزش خوبتون.
بنده ماتریس های فضا ی حالت مربوط به مدل کامل خودرو را استخراج نموده ام و lmi را برای آن حل کرده ام، ولی وقتی ورودی جاده تصادفی به سیستم میدهم خطا زیر
(Assignment has more non-singleton rhs dimensions than non-singleton subscripts) ظاهر می شود. ورودی جاده را از روش های آ»وزش داده شده توسط جنابعالی به سیستم می دهم. لطفا بفرمایید مشکل بنده از کجاست.
با تشکر فراوان
علی جوادی
@غلامرضا بامی محمدی,
این خطا مربوط به پروفایل جاده یا شبیه سازی سیستم نیست. احتمالا یه جایی یک بردار رو میخواهید تو یه بردار دیگه که هم سایز نیستند جاگذاری کنید. خط به خط اجرا کنید تا خطا رو پیدا کنید و درستش کنید. شاید اطلاعات لینک زیر هم کمک کنه:
https://goo.gl/rk7yk6
غلامرضا بامی محمدی
با تشکر از حسن توجه جنابعالی
پیام
با سلام
اگر در سیستمی نویز فرایند، نویز اندازه گیری و عدم قعطیت (نامعینی پارامتری سیستم) داشته باشیم، میتوانیم از کنترلر مقاوم در طراحی کنترلر استفاده کنیم و پلنت را طوری کنترل کنیم که اثرنویز فرایند، نویز اندازه گیری و عدم قعطیت در خروجی کاهش یابد ؟
علی جوادی
@پیام,
اگر نویزها رو به عنوان اغتشاشهای دارای نرم محدود فرض کنیم، امکانش هست
یزدان
با سلام و وقت بخیر خدمت شما
سوالی که داشتم این هست که من طبق توضیحات شما در سری فیلم های مربوط به LMI ، حلگر YALMIP رو نصب کردم بعدش M-file مربوط به مثالی که شما در این سری فیلم ها نوشتید رو تا قسمت حل LMI عینا کپی – پیست کردم و برای گاما = 15 گذاشتم که حل بشه مشکلی که هست اینه که جواب OK میشه ولی اعداد مربوط به ماتریس های A_hat و … نسبت به چیزی که توی فیلم هست خیلی بزرگتر در میاد میخواستم بدونم چه دلیلی داره همون کد جواب دیگه ای میده
با تشکر از توجه شما
علی جوادی
@یزدان,
با سلام
اولا که یالمیپ حلگر نیست و تولباکسه. حلگر الگوریتم مورد استفاده در تولباکس یالمیپ هستش مثل mosek و …
حالا اگر مثل من از حلگر mosek استفاده بکنید به جوابی مشابه (و نه دقیقا یکسان) پاسخهای داخل فیلم می رسید. البته اگر حلگر شما mosek نباشه ولی feasible شده باشه مشکلی وجود نداره. البته ممکنه با mosek به گامای کمتر از حلگرهای دیگه برسید چون mosek معمولا نسبت به بقیه جوابهای خوبی داره و به صورت پیش فرض توسط یالمیپ استفاده میشه (البته اگه نصب شده باشه)
یزدان
حق با شما بود حلگر Mosek رو استفاده کردم مشکلم برطرف شد بازم از پاسخ گویی سریعتون سپاسگزارم.
علی جوادی
@یزدان,
خوشحالم که جواب گرفتید
موفق باشید
hengameh
سلام، می خواستم بپرسم که اگر تو همین سیستم تاخیر در ورودی کنترلی داشته باشیم چه تاثیری روی روابط خواهد داشت ؟ اگر در مورد کنترلرH2/H-infinity هم مطلبی تو سایت بگذارید ممنون میشم.
علی جوادی
@hengameh,
سلام
بحث تاخیر خیلی مفصله. برنامه اینه که بعد تموم شدن تخمین بهینه حالت بحث تاخیر رو شروع کنم. بعد از اینکه خود تاخیر بحث شد، احتمالا ترکیبش با کنترل مقاوم رو هم اشاره بکنم. همچنین ترکیب H2/H-inf هم جزو برنامه های بعدیه. امیدوارم فرصت بکنم و به زودی همه این مباحث رو پوشش بدم
لطفا کمی صبور باشید
امیر
با سلام
بنده قصد شبیه سازی مقاله ای در خصوص
Active Disturbance Rejection Control
که در حوزه کنترل مقاوم است رو دارم. عنوان این مقاله:
Combined feedforward and model-assisted active disturbance
rejection control for non-minimum phase system
هست. در صفحه 4 و 5 این مقاله اثبات روابطی آورده شده و از آنجاییکه بنده با کنترل مقاوم آشنایی ندارم(قدرتی هستم)، خواستم که در صورت امکان بفرمایید کدام یک از فایل های آموزشی شما توضیحات کاملی در خصوص این مطلب ارائه دادن؟
سپاسگزارم
علی جوادی
@امیر,
سلام
مقاله ای که اشاره کردید از یک قسمت feedforward هم استفاده کرده ولی کنترل کننده هایی که من داخل آموزشها استفاده کردم فقط شامل feedback هستند. از طرف دیگه تحلیل پایداری در این مقاله در حوزه فرکانسه در حالیکه من از تحلیل پایداری لیاپونوف استفاده کردم. به نظرم باید روی خود مقاله و مراجعش تمرکز کنید و فیلمهای موجود کمکی بهتون نمیکنه
موفق باشید
یزدان
با سلام خدمت شما
ضمن تشکر بسیار بخاطر تدریس بی نقص و عالیتون ، سوالی که داشتم این هست که اگر بخواییم نویز ناشی از سنسورهای اندازه گیری رو در سیستم کم بکنیم به غیر از فیلتر کردن سیگنال های اندازه گرفته شده ، آیا با روش H بینهایت هم میشه بدون فیلتر کردن به این هدف رسید یعنی علاوه بر اغتشاش سیستم به نویز هم مقاوم باشه ، اگر در این زمینه مقاله یا منبع مناسبی هست و بتونید بهم معرفی کنید بی اندازه سپاگزار خواهم بود
با تشکر فراوان از شما
علی جوادی
@یزدان,
با سلام و تشکر از لطف شما
برای هر سیگنالی که نرم L2 محدود باشه، میشه از روش H بینهایت برای کاهش اثرش استفاده کرد از جمله نویز اندازهگیری سفید.
البته در فرمولبندی کلی H بینهایت میتونید نویز اندازهگیری رو داخل بردار اغتشاش کلی جا بدید و از روش H بینهایت اثر کل بردار اغتشاش (که داخلش نویز اندازهگیری هم هست) رو کم بکنید. مثلا داخل مقاله Doyle شکل سیستم فرض شده رو ببینید:
http://ieeexplore.ieee.org/document/29425/
یزدان
@علی جوادی,
از حسن توجه شما بسیار سپاس گزارم و براتون آرزوی بهترین ها رو دارم.
مریم
با سلام و خسته نباشید
اگر من اثبات روابط LMI و کدهای نوشته شده اش را برایتان میل کنم، با پرداخت هزینه اش علت infeasible بودن مسئله رو حل میکنید؟
علی جوادی
@مریم,
سلام
لطفا با مدیر سایت تماس بگیرید
۰۹۱۶۲۹۶۳۸۷۰
amin
با سلام
اگه یه ماتریس lmi شدنی(feasible) نشه، چیکار کنم فیزیبل شه؟ با تغییر ثابتها یا ماتریس های فضای حالت سیستم میشه فیزیبل کرد؟
در واقع یه مقاله دارم مینویسم مقاله تموم شده همه جاش رو نوشتم حالا که آخرین مرحله اومدم یه مثال شبیه سازی کنم lmi فیزیبل نمیشه
علی جوادی
@amin,
سلام
دقیقا رقابت سر اینه که مساله رو طوری فرمولبندی کنیم که برای سیستمهای مختلف با فضای حالت دلخواه feasible بشه. بعضی LMI ها برای سیستمهای پایدار جواب میدن و بعضیها برای بعضی سیستمهای ناپایدار هم جواب میدن. روش استاندارد و روتین برای feasible کردن LMI وجود نداره و باید روشهای مختلفی که برای مساله خودتون داخل مقالات دیدید امتحان کنید. اگر برای سیستم مورد نظر LMI شما feasible نشه، یعنی روش شما برای اون سیستم قابل پیادهسازی نیست اگرچه ممکنه با تغییر فرمولبندی بشه یک LMI ارائه کرد که برای اون سیستم خاص feasible بشه
رضا
سلام
با تشکر از سایت خوبتون و مطالب خوبی که ارائه می دید.
سوالی که از خدمتتون دارم اینه که چرا LMI های مربوط به کنترل H2 و MIX رو در ادامه آموزش هاتون قرار ندادید؟
اگر این بخش رو هم آموزش بدید ممنون می شم
علی جوادی
@رضا,
با سلام و تشکر از لطف شما
طبق برنامه در آینده این دو موضوع رو هم پوشش خواهم داد ولی فعلا باید فیلمهای آموزشی تخمین بهینه حالت رو تموم کنم.
منتظر باشید