فیلمهای مربوط به کنترل مقاوم فیدبک حالت سیستمهای خطی تحت اغتشاش و همچنین کنترل فیدبک خروجی سیستمهای خطی با استفاده از رویتگر قبلا خدمت دوستان تقدیم شده است. اگر سیستمی هم تحت تاثیر اغتشاش خارجی بوده و هم امکان اندازهگیری تمامی حالتها وجود نداشته باشد، دیگر نمیتوان از این فیلمها برای چنین سیستمی استفاده کرد. در سری فیلمهای حاضر دقیقا این مشکل مدنظر قرار گرفته و هدف طراحی یک کنترلکننده مقاوم برای سیستمهای خطی تحت تاثیر اغتشاش فقط با استفاده از یک یا چند خروجی سیستم است. کنترل کننده مورد نظر دارای رویتگر نبوده ولی دارای دینامیک داخلی است. همچنین تنها از خروجی سیستم فیدبک گرفته شده و نیازی به ورودی سیستم تحت کنترل ندارد. معیار تضعیف اغتشاش همان نرم ∞H است که به تفصیل در سری فیلمهای کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی تشریح شده و ارتباط آن با تلف کنندگی (Dissipativity) و پایداری بهره L2 بحث شده است. برای اطلاعات بیشتر در مورد تضعیف اغتشاش از طریق نرم ∞H و مزایای فرمولبندی این مساله به شکل LMI به فیلمهای مربوط به کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی مراجعه کنید.
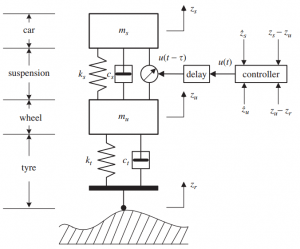
بعد از محاسبه نامساویهای ماتریسی خطی لازم برای حل مساله که ایده اصلی آن از یک مقاله IEEE گرفته شده است، روش پیشنهادی بر روی یک مدل یک چهارم سیستم تعلیق خودرو پیاده شده و سیستم حلقه بسته هم در محیط m-file و هم در سیمولینک شبیهسازی شده است. همچنین توابع تبدیل از نویز اندازه گیری، اغتشاش خارجی و ورودی مرجع به خروجی محاسبه شده و پهنای باند سیستم حلقه بسته و خواص تضعیف نویز و اغتشاش به صورت تحلیلی و شبیهسازی مورد بررسی قرار گرفته است. لازم به ذکر است که سیستم تعلیق در این سری فیلمها فقط به عنوان یک مثال کاربردی مورد استفاده قرار گرفته است و توضیح اضافی در مورد آن ارائه نشده است. برای درک بهتر این مثال شاید بهتر باشد قبل از دیدن این سری فیلمها، جلسات مربوط به مدلسازی و شبیهسازی ارتعاشات جاده برای سیستم کنترل تعلیق فعال خودرو را ملاحظه کنید و بعد از اینکه با سیستم تعلیق آشنا شدید، این سری فیلمها را ببینید.
با امید به اینکه مورد رضایت شما عزیزان قرار بگیرد
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
فرمولبندی طراحی کنترل مقاوم فیدبک خروجی برای سیستمهای دارای اغتشاش خارجی
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
پیادهسازی کنترلکننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیهسازی در متلب
شبیهسازی در محیط سیمولینک و تحلیل در حوزه فرکانس
جلسه دوم:
جلسه سوم:
جلسه چهارم:
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم


حسام
سلام آقای دکتر. وقت شما بخیر.
در مسائل ردیابی با استفاده از روشی که شما ارائه کرده اید، آیا پایداری سیستم برای ردیابی تضمین می شود؟
چون در واقع مساله تنظیم را حل می کنیم و به مساله ردیابی تعمیم می دهیم.
ممنونم از شما استاد گرامی
alij63@gmail.com
سلام
بله. قضیه لیاپونوف پایداری رو تضمین میکنه
علی
سلام
آیا رویتگری هم وجود دارد که بتواند نسبت به نامعینی مقاوم باشد؟
برای یک سیستم که نامعینی پارامتری دارد کنترل کننده مقاوم طراحی کردم و حالا قصد دارم که از یک رویتگر برای تخمین حالت ها استفاده کنم.
alij63@gmail.com
سلام
تو نت سرچ کنید قطعا پیدا میشه
هادی
سلام استاد. خسته نباشید.
دو سوال داشتم از خدمتتان.
1-با توجه به این که در کنترل کننده های دینامیکی، ما درجه آزادی بیشتری نسبت به کنترل کننده استاتیکی برای طراحی داریم. طبیعتا باید انتظار جواب های مناسبت تری در استفاده از کنترل کننده دینامیکی داشته باشیم. درست است؟
2- اگر از کنترل کننده فیدبک حالت دینامیکی استفاده کنیم (یعنی با وجود این که حالت ها را داشته باشیم، باز هم از کنترل کننده دینامیکی استفاده کنیم)، باز هم درجه آزادی بالاتر می رود. آیا استفاده از چنین کنترل کننده ای منطقی است؟
سپاسگزارم
alij63@gmail.com
سلام
خیر. فیدبک خروجی دارای یهره های بیشتر هست ولی دلیل نمیشه بهتر باشه چون تعداد حالتهای کمتری نسبت به فیدبک حالت اندازه گیری میشه و بنابراین اطلاعات از سیستم کمتره.
همیشه درجه آزادی بیشتر مزیت نیست. اگر امکان داشته باشه، بهتره خود حالتها همگی اندازه گیری بشه
هادی
ممنونم بابت پاسختان دقیق تان.
در صورتی که حالت های سیستم را به طور کامل در اختیار نداشته باشیم، به نظر شما بهتر است از کنترل کننده دینامیکی خروجی استفاده شود یا از کنترل کننده مبتنی بر رویتگر؟
در شرایط یکسان کدام یک ارجحیت دارد؟
متشکرم
alij63@gmail.com
میتونید باهم مقایسه کنید. نمیشه قانون کلی ارائه داد
حمید
سلام آقای دکتر. وقت شما بخیر.
یک سوال داشتم از خدمتتان.
آیا مفهوم کلمه uncertainty با perturbation متفاوت است؟ یعنی اگر در سیستمی perturbation وجود داشته باشد، می توان تحت عنوان نامعینی در نظر گرفت؟
با سپاس
علی جوادی
سلام
بهتره به همون مرجعی که دیدید مراجعه کنید و مفهوم کلمات رو ازش استخراج کنید.
ممکنه یه جایی این دو تا معنی یکسان داشته باشند ولی جای دیگه یکی نباشند
حمید
سلام مجدد آقای دکتر. ممنونم بابت وقتی که گذاشتید.
عذر خواهم سوال دیگری هم ازخدمتتان دارم.
در حالت کلی این دو کلمه چه تفاوتی با هم دارند؟
سپاسگزارم از شما
علی جوادی
همونطور که گفتم به مرجع مربوطه باید مراجعه کنید
علی
سلام – ببخشید کلا 6 مجموعه آموزش کنترل مقاوم دارید، اینها کل کنترل مقاوم دوره ارشد رو پوشش می دهند؟ البته اینکه با روش LMI است خیلی خوبه – با تشکر
علی جوادی
سلام. بله 6 مجموعه هست ولی طبق سرفصلهای معمول که در دانشگاه تدریس میشه نیست و برای پاس کردن درس کنترل مقاوم کافی نیست.
بیشتر برای مقاله کار کردن مناسبه
محمدرضا
با سلام و تشکر فراوان از لطف شما
سیستمی که من مدل سازی میکنم یک سیستم چند درجه آزادیه یعنی متغیرهای حالت به هم وابسته هستن و ماتریس سیستم قطری نیست. .برای چنین سیستمی فیلم آموزشی یا راهکاری هست که منو راهنمایی بفرمایید؟
علی جوادی
سلام
محدودیتی برای ماتریس سیستم وجود نداره و میتونید از همین LMI ها استفاده کنید
الیاس
با عرض سلام و خسته نباشید.
سوالی داشتم از خدمتتان.
روش کنترل Hinf به ما می گوید، نسبت L2 خروجی کنترل شده به اغتشاش کوچکتر از گاما است. ولی اگر اغتشاش موجود در سیستم، در لحظات ابتدایی تقریبا صفر باشد، این نسبت در همان لحظات، بسیار زیاد می شود. و از گاما فراتر می رود، چگونه می توان این سوال را توجیه کرد؟
با سپاس از شما استاد گرامی
علی جوادی
نرم L2 اغتشاش هیچوقت صفر نیست و اگر صفر باشد یعنی اغتشاش نداریم و نیازی به کنترل مقاوم نیست
امین
سلام آقای دکتر. ممنونم بابت تدریس بی نظیرتون.
آیا استفاده از Schur complement ممکن است باعث محافظه کاری شود؟
با سپاس
علی جوادی
سلام
خیر چون دو عبارت معادل هم هستند
جواد
با سلام مجدد و تشکر از آقای مهندس جوادی بابت پاسخ کاملشان
بنده رشته ام مهندسی عمران هست خیلی ممنون میشم شکل ماتریس های LMI را در حالتی که ماتریس های (C1,D11,D12,C2,D21,D22) همه اشان وجود دارند را برایم ایمیل نمایید تا بنده مقایسه کنم که روابطم درست باشند و به همان ماتریس های ارسالی شما برسم. قبلا از آموزش خوب شما جناب آقای مهندس جوادی تشکر می کنم.
ایمیل بنده : matlab.tabriz@gmail.com
علی جوادی
من با در نظر گرفتن همه ماتریسها LMI ها رو بدست نیاوردم و فقط همون نتایجی که در فیلمها میبینید رو دارم.
با همون روند موجود در آموزشها جلو برید و همه ماتریسها رو در نظر بگیرید
جواد
با سلام و تشکر از آموزش بسیار خوب و کاربردی آقای مهندس جوادی
بنده یک سوالی داشتم ممنون میشم راهنمایی بفرمایید. ماتریس های LMI را در حالتی که ما در معادله خروجی هدف و در معادله خروجی اندازه گیری شده همه ماتریس ها را داشته باشیم (C1,D11,D12,C2,D21,D22) به چه شکلی در برنامه متلب بنویسیم که کلی باشد. یکی از خروجی های مساله بنده شتاب هست که به صورت تابعی از اغتشاش خارجی و نیروی کنترلی می باشد برای همین منظور ماتریس های (C1,D11,D12,C2,D21,D22) همشون در معادله سیستم ظاهر می شوند. با تشکر از راهنمایی های شما
علی جوادی
با سلام و تشکر از لطف شما
برای ساده سازی شاید بعضی جاها من بعضی ماتریسها رو صفر در نظر گرفته باشم اما میتونید با همون روندی که داخل فیلمها هست جلو برید و اون ماتریسها رو غیرصفر در نظر بگیرید.
در اینصورت نامساویهای بدست اومده متفاوت هستند و شامل اون ماتریسها خواهد بود