احتمالا برای شما هم پیش اومده که در یک مقاله یا کتاب به جایی رسیدید که باید یک ناتساوی ماتریسی خطی (یا LMI) رو حل کنید و در بدر دنبال یک نفر هستید تا در کوتاهترین زمان ممکن حل این نوع ناتساوی ها رو به شما یاد بده تا مجبور نباشید زمان قابل توجهی صرف کنید و از منابع مختلف دنبال راه حل باشید. اگر شما هم جزو این دسته از محققین هستید دیگه نگران نباشید. در این پست قراره تمام جزییات و کلیات نامساوی ماتریسی خطی (و حتی غیرخطی) با نحوه حل اونها در متلب و با دو روش تولباکس متلب و YALMIP به روش ساده و با مثالهای مفصل توضیح داده بشه. اگر با این فیلمهای آموزشی همراه شده و مرحله به مرحله مثالها رو پیش برید بعد از این 11 جلسه قادر خواهید بود حل کننده (solver) مناسب رو برای مساله خودتون انتخاب کرده و ناتساویهای ماتریسی خودتون رو باهاش حل بکنید. بعد از تشریح کامل دو روش بالا یک مثال از طراحی کنترل کننده برای سیستم شناور مغناطیسی از یک مقاله IEEE با استفاده از LMI خدمت شما ارایه میشه (به همراه شبیه سازی در محیط سیمولینک) تا مطلب کامل جا بیافته. با ما همراه باشید…
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری سیستمهای کنترل خطی – آشنایی با کدنویسی در محیط متلب
جلسه اول: مقدمات ریاضی و تعریف ناتساوی های ماتریسی
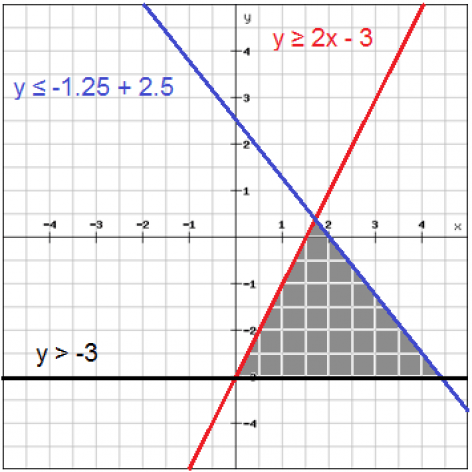
در این جلسه ابتدا مقدمات ریاضی و تعریف ناتساوی های ماتریسی به همراه مفاهیم مجموعه های محدب و نامحدب توضیح داده میشه و چند مثال هم از هر دو نوع مجموعه ارایه میشود. سپس نحوه تبدیل ناتساویهای خام به حالت استاندارد تشریح شده و در انتها روشهای مختلف حل عددی ناتساویهای ماتریسی به طور خلاصه مطرح میشود. جهت ارزیابی شما عزیزان جلسه اول رایگان تقدیم میشود.
مدت زمان آموزش: 49 دقیقه
محتویات درس: فیلم با کیفیت 720p و پاورپوینت درس
حجم فایل: 65 مگابایت
پیش نمایش جلسه اول:
جلسه دوم: تعیین متغیرهای ماتریسی و وارد کردن جملات LMI در تولباکس متلب
در این جلسه کار با تولباکس LMI متلب را شروع کرده و مراحل مختلف ایجاد یک LMI ارایه میشود. به طور خاص نحوه تعیین متغیرهای ماتریسی و همینطور نحوه وارد کردن جملات داخلی و خارجی به همراه مثال در محیط متلب تشریح میشود.
مدت زمان آموزش: 69 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس- کد متلب مربوط به مثالها- فایل pdf راهنمای استفاده از تولباکس متلب و لیست مرتب شده تمام دستورات مرتبط با تولباکس LMI متلب
حجم فایل: 89 مگابایت
پیش نمایش جلسه دوم:
جلسه سوم: معرفی دستور feasp تولباکس متلب جهت حل LMI
در این جلسه دستورات مختلفی که برای کسب اطلاعات تکمیلی از متغیرها و LMI های تعریف شده در متلب وجود دارند بررسی شده و با مثال تشریح می شوند. در ادامه یکی از دستورات مهم تولباکس LMI متلب که برای حل مسایل ناتساوی مورد استفاده قرار میگیرد معرفی شده و یک مثال از تحلیل پایداری سیستم کنترلی برای آن ارایه میشود.
مدت زمان آموزش: 68 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 100 مگابایت
پیش نمایش جلسه سوم:
جلسه چهارم: معرفی دستورات mincx و gevp تولباکس متلب جهت حل مسایل مینیممسازی
در این جلسه ابتدا دستور mincx که برای حل ناتساویهای ماتریسی با شرط مینیمم سازی (یا ماکزیمم سازی) استفاده میشود به طور کامل تشریح شده و مثال جلسه قبل با شرط مینیمم و ماکزیمم سازی دوباره با این دستور حل میشود. همچنین دستور gevp که مربوط به حل مسایل مینیمم سازی مقدار ویژه تعمیم یافته میباشد تشریح میشود.
مدت زمان آموزش: 51 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 69 مگابایت
پیش نمایش جلسه چهارم:
جلسه پنجم: طراحی کنترل کننده فیدبک حالت برای سیستم خطی و حل LMI های آن با تولباکس متلب
در این جلسه ابتدا دستورات باقیمانده که مربوط به ارزیابی LMI بعد از حل آن است معرفی میشوند. در ادامه یک مثال از طراحی کنترل کننده فیدبک حالت برای سیستم خطی به شکل LMI فرمول بندی شده و با تولباکس LMI متلب حل میگردد. نهایتا دو ترفند بسیار پرکاربرد تبدیل متجانس (Congruent transformation) و لم شور (Schur complement) برای LMI بیان میشوند.
مدت زمان آموزش: 53 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 76 مگابایت
پیش نمایش جلسه پنجم:
جلسه ششم: معرفی تولباکس یالمیپ برای حل LMI و نجوه دانلود و نصب آن
از این جلسه معرفی تولباکس YALMIP شروع میشود و ابتدا توضیحات مقدماتی درباره آن و مزایای آن نسبت به تولباکس متلب ارایه میشود. در ادامه تمامی مراحل دانلود و نصب این تولباکس بر روی متلب به صورت گام به گام تشریح میشود. در انتها نحوه ارزیابی نصب درست تولباکس و solver های موجود در آن توضیح داده میشود.
توجه: اخیرا ظاهر و پوسته سایت YALMIP دچار تغییر و تحول شده و با صفحات نشان داده شده در فیلمهای حاضر قدری متفاوت است. با توجه به اینکه محتویات سایت YALMIP تغییر پیدا نکرده و تنها محل لینکها تغییر پیدا کرده (مثلا لینکهای ستونی سمت چپ به بالای صفحه انتقال پیدا کرده)، فیلمهای موجود دوباره ضبط نشده و همین فیلمها قابل استفاده هستند.
مدت زمان آموزش: 47 دقیقه
محتویات درس: فیلم آموزشی
حجم فایل: 96 مگابایت
پیش نمایش جلسه ششم:
جلسه هفتم: تعریف متغیرهای ماتریسی و قیدها با استفاده از تولباکس یالمیپ
در این جلسه ابتدا نحوه تعریف متغیرهای ماتریسی با مثالهای متنوع در محیط متلب توضیح داده شده و سپس چگونگی تعریف قیدها یا همان ناتساویهای ماتریسی جهت استفاده در YALMIP با چندین مثال تشریح میشود.
مدت زمان آموزش: 62 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 85 مگابایت
پیش نمایش جلسه هفتم:
جلسه هشتم: تعریف تابع هزینه و حل LMI با استفاده از تولباکس یالمیپ
در این جلسه نحوه تعریف تابع هزینه، گزینه های اختیاری مربوط به YALMIP (به جز solver ها)، چگونگی حل مساله و در نهایت روش استخراج متغیرهای ماتریسی تشریح شده و مثال تحلیل پایداری که جلسات پیش با تولباکس متلب حل شده بود، با YALMIP هم حل میشود.
مدت زمان آموزش: 71 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 114 مگابایت
پیش نمایش جلسه هشتم:
جلسه نهم: معرفی و تشریح نحوه دانلود و نصب سه solver پرکاربرد به نامهای PENBMI ، SDPT3 و MOSEK
مباحث باقیمانده از توضیحات مربوط به YALMIP از جمله solver ها (داخلی و خارجی) در این جلسه مورد بحث قرار میگیرد. به طور خاص نحوه دانلود و نصب سه solver پرکاربرد به نامهای PENBMI ، SDPT3 و MOSEK به طور کامل تشریح شده و مثال تحلیل پایداری سیستم خطی که در جلسات قبل با تولباکس متلب حل شده بود، با این سه solver نیز حل میگردند.
مدت زمان آموزش: 73 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 169 مگابایت
پیش نمایش جلسه نهم:
جلسه دهم: معرفی دینامیک غیرخطی قطار مغناطیسی شناور و خطیسازی حول نقطه کار
در این جلسه تکنولوژیهای موجود در ساخت قطارهای مغناطیسی معرفی شده و دینامیک غیرخطی شناورسازی یک قطار مغناطیسی با تکنولوژی EMS از یک مقاله IEEE ارایه میشود. در ادامه نقاط تعادل و نامی دینامیک استخراج شده و حول نقطه مورد نظر خطیسازی ژاکوبی انجام میشود تا ماتریسهای مورد نیاز برای طراحی کنترلکننده فیدبک حالت بدست آورده شود.
مدت زمان آموزش: 66 دقیقه
محتویات درس: فیلم آموزشی و کلیپی کوتاه از عملکرد قطار مغناطیسی- فایل پاورپوینت و مقاله IEEE حاوی دینامیک شناورسازی قطار مغناطیسی
حجم فایل: 116 مگابایت
پیش نمایش جلسه دهم:
جلسه یازدهم: طراحی و شبیهسازی فیدبک حالت برای سیستم شناور مغناطیسی
در این جلسه ابتدا دینامیک غیرخطی شناور مغناطیسی در محیط متلب و در نقطه کار دلخواه خطی شده و سپس با هر دو روش تولباکس LMI متلب و YALMIP مساله پایدارسازی سیستم خطی شده با فیدبک حالت حل میشود. همچنین بعد از بدست آوردن بهره کنترل کننده با استفاده از solver های PENBMI، SDPT3 و MOSEK در محیط YALMIP و بهره بدست آمده از تولباکس متلب، سیستم حلقه بسته (با دینامیک غیرخطی) در محیط سیمولینک شبیه سازی شده و نتایج حاصل از این بهره ها باهم مقایسه شده است.
مدت زمان آموزش: 67 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کدها و فایلهای شبیه سازی سیستم حلقه بسته
حجم فایل: 113 مگابایت
پیش نمایش جلسه یازدهم:
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



یاسمن
اوکی
سپاس
ببخشید یک سوال دیگه:
یکی از درایه های ماتریس من در ناتساوی ماتریسی به صورت+( P(UA)+TC)’ P(UA)+TC که من بصورت زیر اجرا کردم
lmiterm([2 1 1 P],U*A,1,’s’);
%lmiterm([2 1 1 0],T*C);
%lmiterm([2 1 1 0],C’*T’);
اما دو خطی که با % نشان دادم رو ایراد میگیره که ابعاد متناسب نیستن! بنظرتون مشکل رو چطور حل کنم؟
از اینکه باز هم راهنمایی می فرمایید سپاسگزارم.
علی جوادی
@یاسمن,
با فرض اینکه ابعاد تمام ماتریسها درست تعیین شده باشند، به نظر میرسه مشکل تو خط اوله. مساله اینجاست که ماتریس UA از سمت راست به P ضرب شده ولی تو خط اول طوری تعریف کردید که انگار ماتریس UA از سمت چپ به ماتریس P ضرب شده. در واقع باید جای UA و 1 تو تعریف عوض بشه.
یاسمن
سلام
وقت بخیر
متاسفانه من دیر پاسخ شما رو دیدم،واقعا سپاسگزارم. روش پیشنهادی شما رو انجام میدم، امیدوارم به جواب برسه. فقط ep1 و ep2 رو بنظرتون به چه صورتی تعریف کنم؟در واقع مساله LMI با فرض مینیمم کردن ep ها باید باشه !
با آرزوی سلامت و شادی براتون
علی جوادی
@یاسمن,
سلام
همونطور که قبلا عرض کردم علاوه بر ماتریس مجهول Z باید ep1>0 و ep2>0 رو هم به عنوان دو مجهول اسکالر تعریف کنید و بعد دو تا LMI بدست اومده رو با شرط مینیمم سازی c1*ep1+c2*ep2 حل کنید که c1 و c2 دو عدد مثبت هستند که شما انتخاب می کنید. البته دو شرط مثبت بودن ep1 و ep2 رو هم باید به LMI های قبلی اضافه کنید.
یاسمن
سلام
سپاس از توضیحتون
ماتریس u 7×6 و ماتریس v 7×4 هستش، یعنی ماتریس A 7×10 میشه
راستش هنوز نمیدونم چه راهی مناسب تره، و چه راه حلی بدون تبدیل به نامساوی میتونه براش وجود داشته باشه، باز هم ازتون خواهش میکنم اگر نکته ای در این خصوص به ذهنتون رسید، بفرمائید.
صمیمانه سپاسگزارم
علی جوادی
@یاسمن,
سه نکته زیر رو هم به پاسخ قبلی باید اضافه کنم:
1) به جای تجزیه ماتریسها میتونید از تعریف متغیرهای جدید بهره ببرید. فرض کنید متغیر جدید مساله [Z=[U V بوده و ماتریس جدید [N=[M;C رو هم تعریف کنید (ماتریس C زیر ماتریس M قرار دارد). بدین ترتیب میشه تساوی اول رو به شکل (Z=A+T(I-W و دومی رو به شکل ZN=I نوشت. حال اگر این دو تساوی رو به شکل ناتساوی بنویسیم داریم:
ep1*I<ZN-I<ep1*I-
ep2*I<Z-A-T(I-W)<ep2*I-
حالا میتونید دو LMI بالا رو نسبت به متغیر جدید Z حل کرده و پس از حل مساله با توجه به ابعاد ماتریسهای U و V از داخل ماتریس Z استخراج کنید. دقت کنید که ابعاد ماتریسهای همانی درست باشند.
2) هر دوی ep1 و ep2 باید اسکالرهای مثبتی باشند.
3) به جای مینیمم کردن ep1+ep2 میتونید c1*ep1+c2*ep2 رو مینیمم کنید که در اون c1 و c2 اعداد مثبتی هستند که شما میتونید انتخاب کنید. این پارامترهای آزاد وزنی کمک میکنند تا اهمیت ep1 و ep2 رو مشخص کنید. مثلا اگر c1 بزرگتر از c2 باشه، یعنی اینکه ناتساوی اول (بدست اومده از تساوی اول) برای شما اهمیت بیشتری داره و میخوایید ep1 خیلی نزدیک صفر باشه (نسبت به ep2) تا ناتساوی اول بیشتر به تساوی نزدیک بشه.
موفق باشید
یاسمن
سلام
وقت بخیر
باز هم از تدریس خوب LMI تشکر میکنم و یک سوال داشتم
رابطه تساوی ماتریسی به شکل زیر دارم، میخواستم ببینم امکان حلش با YALMIP وجود داره؟
[U V]=A+T(I-W) و UM+VC=I که T، ماتریس دلخواهی است و A,W,M,C هم ماتریس هستند و موجود. و هدف بدست آوردن ماتریس هایU,V هستش.
از اینکه راهنمایی می فرمایید سپاسگزارم.
علی جوادی
@یاسمن,
با سلام و وقت بخیر.
۱) با توجه به اینکه مساله شما تساوی ماتریسی است و ناتساوی نیست شاید بهتر باشه از روشهای دیگه (اگر موجود باشه) استفاده کنید.
۲) توصیه میشه همیشه مساله رو از اول به شکل LMI مدل کنید تا اینکه مساله رو به شکل تساوی بدست بیارید و بعد سعی کنید با یک تولباکس که برای حل ناتساوی بهینه شده حل بکنید. شبیه اینه که شما بخواهید مثلا معادله جبری لیاپونوف یا معادله ریکاتی رو با LMI حل کنید درحالی که کلی روشهای حل عددی برای این معادلات وجود دارند. اگر هنوز اصرار به حل مساله با یالمیپ دارید به گزینه سه عمل کنید (که تضمینی براش وجود نداره).
۳) متاسفانه در مورد ابعاد ماتریسها اصلا صحبتی نکردید که باعث ایجاد ابهام میشه. مثلا معلوم نیست منظور از معادله U V]=A+T(I-W)] چیه؟ اگر منظور اینه که ابعاد U و V باهم با ابعاد A یکسانه بنابراین اولا باید ماتریس A و همچنین (T(I-W رو بگونهای تجزیه بکنید که عبارتی به شکل [U V] ظاهر نشه. ثانیا باید تساویها رو به ناتساوی تبدیل کنید (البته بعد از تجزیه)، مثلا به شکل زیر:
ep1*I<UM+VC-I<ep1*I-
ep2*I<[U V]-A-T(I-W)<ep2*I-
به شرطی که مثلا ep1 + ep2 مینیمم بشه. در حالت ایدهال که ep1=ep2=0 بشه، مساله تساوی حل میشه ولی در صورت وجود جواب یکتا برای این تساویها یالمیپ به احتمال زیاد اعداد کوچکی برای این متغیرها پیدا خواهد کرد که اگر به اندازه کافی کوچک باشند، به جواب ایدهال بسیار نزدیک خواهد بود.
امیدوارم این توضیحات کافی باشه
رضا
با سلام و احترام
مطالب ارائه شده بسیار مفید و کاملا عملی هستند.
تسلط علمی مدرس نیز بر روی مطالب در تمامی جلسات مشهود است.
جا داره واقعا از تسلط و توضیحات دقیق شما تشکر کنم.
با آرزوی موفقیت و سربلندی … .
مدیر سایتادمین سایت ( مالک تایید شده )
@رضا,
سلام
من به ایشون اعتقاد زیادی دارم نظمشون زبان زد خاص و عامه
درود
محمد جواد
ممنون از راهنماییتون مشکل حل شد . کیفیت صدا و تصویر و آموزش هم خیلی خوب بود.
مدیر سایتادمین سایت ( مالک تایید شده )
@محمد جواد,
نظر لطف شماست.
ممنون که اطلاع دادید مشکلتون برطرف شده.
محمد جواد
سلام من فیلم رو دانلود کردم ولی هر کاری میکنم از حالت زیپ خارج نمیشه ؟ میشه راهنمایی بفرمایید؟
مدیر سایتادمین سایت ( مالک تایید شده )
@محمد جواد,
سلام
همه پارت ها رو توی یک فولدر قرار بدین و بعد روی یکی از اونها کلیک راست کنید و گزینه اکسترکت هیر رو بزنید.
یاسمن
درود به شما
جلسه دوم LMI هم مثل جلسه اول خیلی خوب بود، هیچ مشکلی هم در پخش نبود. اساسی خدا قوت.
فقط اگر فونت دستورات matlab رو بزرگتر می گذاشتید بنظرم بهتر دیده می شد.
سلامت و پاینده باشید.
علی جوادی
@یاسمن, ممنون از لطف شما و خوشحالم که فایلهای ویدیویی مشکلی ندارند. متاسفانه ضبط تمامی جلسات مربوط به آموزش LMI به اتمام رسیده و در این مرحله قادر به تغییر فونت دستورات متلب نیستم و با توجه به اینکه دستورات متلب موجود در فیلم قابل رویت هستند (هرچند کمی کوچک هستند) و همچنین تمامی کدها تقدیم شما میشود، ویدیوها دوباره ضبط نخواهند شد. البته در ویدیوهای آینده حتما پیشنهاد شما مدنظر قرار خواهد گرفت.
با سپاس
علی جوادی
با سلام و تشکر از حسن توجه شما
من فیلم این جلسه رو با پخش کننده های ویدیویی مختلف امتحان کردم و داخل هیچ کدوم تاخیر یا جلو افتادگی وجود نداشت. کیفیت صدای VLC player و media player classic کمی پایین بود، کیفیت تصویر و صدای windows media player خوب بود و KM player هم در همه موارد متوسط بود ولی مشکل عدم مشاهده فایل pdf تو هیچ کدوم مشاهده نشد. البته فایل pdf به همراه فیلم تصویری جلسه دوم روی سایت قرار گرفته است. شاید بهتر باشه که یک نسخه جدید از پخش کننده ویدیویی که استفاده می کنید تهیه کنید و با نسخه جدید امتحان کنید.
با تشکر از نظرتون
یاسمن
سلام
خداقوت
سپاس از کار مثبتی که در حال انجامش هستید.
در مورد آموزش LMI در ابتدای جلسه اول مدرس محترم از فایل pdf ی صحبت می فرمایند که گویا با فرض این است که مخاطبین فایل را مشاهده می کنند ، اما در فیلم فایلی نشان داده نمی شود.
لطفا چک بفرمایید.
هادی
سلام آقای دکتر
آیا YALMIP قابلیت حل مسائل bi-level که مسئله داخلی آن mixed-integer باشد را دارد؟ چون مسئله ای در این زمینه دارم میخواستم ببینم اگر YALMIP قابلیت حل آن را ندارد سراغش نروم. و اگر نرم افزاری میشناسید که اینگونه مسائل را حل میکند ممنون میشوم بگید.
باتشکر
علی جوادی
@هادی,
با سلام
بله با YALMIP میتونید هم مسایل Mixed Integer Linear programming و هم مسایل Mixed Integer Quadratic programming رو حل بکنید. برای این کار میتونید از MOSEK به عنوان solver استفاده کنید که نحوه دانلود و نصبشو تو جلسه نهم به صورت کامل توضیح دادم
درود