احتمالا برای شما هم پیش اومده که در یک مقاله یا کتاب به جایی رسیدید که باید یک ناتساوی ماتریسی خطی (یا LMI) رو حل کنید و در بدر دنبال یک نفر هستید تا در کوتاهترین زمان ممکن حل این نوع ناتساوی ها رو به شما یاد بده تا مجبور نباشید زمان قابل توجهی صرف کنید و از منابع مختلف دنبال راه حل باشید. اگر شما هم جزو این دسته از محققین هستید دیگه نگران نباشید. در این پست قراره تمام جزییات و کلیات نامساوی ماتریسی خطی (و حتی غیرخطی) با نحوه حل اونها در متلب و با دو روش تولباکس متلب و YALMIP به روش ساده و با مثالهای مفصل توضیح داده بشه. اگر با این فیلمهای آموزشی همراه شده و مرحله به مرحله مثالها رو پیش برید بعد از این 11 جلسه قادر خواهید بود حل کننده (solver) مناسب رو برای مساله خودتون انتخاب کرده و ناتساویهای ماتریسی خودتون رو باهاش حل بکنید. بعد از تشریح کامل دو روش بالا یک مثال از طراحی کنترل کننده برای سیستم شناور مغناطیسی از یک مقاله IEEE با استفاده از LMI خدمت شما ارایه میشه (به همراه شبیه سازی در محیط سیمولینک) تا مطلب کامل جا بیافته. با ما همراه باشید…
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری سیستمهای کنترل خطی – آشنایی با کدنویسی در محیط متلب
جلسه اول: مقدمات ریاضی و تعریف ناتساوی های ماتریسی
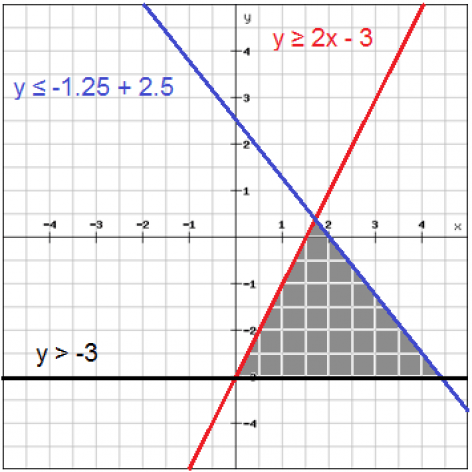
در این جلسه ابتدا مقدمات ریاضی و تعریف ناتساوی های ماتریسی به همراه مفاهیم مجموعه های محدب و نامحدب توضیح داده میشه و چند مثال هم از هر دو نوع مجموعه ارایه میشود. سپس نحوه تبدیل ناتساویهای خام به حالت استاندارد تشریح شده و در انتها روشهای مختلف حل عددی ناتساویهای ماتریسی به طور خلاصه مطرح میشود. جهت ارزیابی شما عزیزان جلسه اول رایگان تقدیم میشود.
مدت زمان آموزش: 49 دقیقه
محتویات درس: فیلم با کیفیت 720p و پاورپوینت درس
حجم فایل: 65 مگابایت
پیش نمایش جلسه اول:
جلسه دوم: تعیین متغیرهای ماتریسی و وارد کردن جملات LMI در تولباکس متلب
در این جلسه کار با تولباکس LMI متلب را شروع کرده و مراحل مختلف ایجاد یک LMI ارایه میشود. به طور خاص نحوه تعیین متغیرهای ماتریسی و همینطور نحوه وارد کردن جملات داخلی و خارجی به همراه مثال در محیط متلب تشریح میشود.
مدت زمان آموزش: 69 دقیقه
محتویات درس: فیلم با کیفیت 720p- پاورپوینت درس- کد متلب مربوط به مثالها- فایل pdf راهنمای استفاده از تولباکس متلب و لیست مرتب شده تمام دستورات مرتبط با تولباکس LMI متلب
حجم فایل: 89 مگابایت
پیش نمایش جلسه دوم:
جلسه سوم: معرفی دستور feasp تولباکس متلب جهت حل LMI
در این جلسه دستورات مختلفی که برای کسب اطلاعات تکمیلی از متغیرها و LMI های تعریف شده در متلب وجود دارند بررسی شده و با مثال تشریح می شوند. در ادامه یکی از دستورات مهم تولباکس LMI متلب که برای حل مسایل ناتساوی مورد استفاده قرار میگیرد معرفی شده و یک مثال از تحلیل پایداری سیستم کنترلی برای آن ارایه میشود.
مدت زمان آموزش: 68 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 100 مگابایت
پیش نمایش جلسه سوم:
جلسه چهارم: معرفی دستورات mincx و gevp تولباکس متلب جهت حل مسایل مینیممسازی
در این جلسه ابتدا دستور mincx که برای حل ناتساویهای ماتریسی با شرط مینیمم سازی (یا ماکزیمم سازی) استفاده میشود به طور کامل تشریح شده و مثال جلسه قبل با شرط مینیمم و ماکزیمم سازی دوباره با این دستور حل میشود. همچنین دستور gevp که مربوط به حل مسایل مینیمم سازی مقدار ویژه تعمیم یافته میباشد تشریح میشود.
مدت زمان آموزش: 51 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 69 مگابایت
پیش نمایش جلسه چهارم:
جلسه پنجم: طراحی کنترل کننده فیدبک حالت برای سیستم خطی و حل LMI های آن با تولباکس متلب
در این جلسه ابتدا دستورات باقیمانده که مربوط به ارزیابی LMI بعد از حل آن است معرفی میشوند. در ادامه یک مثال از طراحی کنترل کننده فیدبک حالت برای سیستم خطی به شکل LMI فرمول بندی شده و با تولباکس LMI متلب حل میگردد. نهایتا دو ترفند بسیار پرکاربرد تبدیل متجانس (Congruent transformation) و لم شور (Schur complement) برای LMI بیان میشوند.
مدت زمان آموزش: 53 دقیقه
محتویات درس: فیلم- پاورپوینت درس و کد متلب مربوط به مثالها
حجم فایل: 76 مگابایت
پیش نمایش جلسه پنجم:
جلسه ششم: معرفی تولباکس یالمیپ برای حل LMI و نجوه دانلود و نصب آن
از این جلسه معرفی تولباکس YALMIP شروع میشود و ابتدا توضیحات مقدماتی درباره آن و مزایای آن نسبت به تولباکس متلب ارایه میشود. در ادامه تمامی مراحل دانلود و نصب این تولباکس بر روی متلب به صورت گام به گام تشریح میشود. در انتها نحوه ارزیابی نصب درست تولباکس و solver های موجود در آن توضیح داده میشود.
توجه: اخیرا ظاهر و پوسته سایت YALMIP دچار تغییر و تحول شده و با صفحات نشان داده شده در فیلمهای حاضر قدری متفاوت است. با توجه به اینکه محتویات سایت YALMIP تغییر پیدا نکرده و تنها محل لینکها تغییر پیدا کرده (مثلا لینکهای ستونی سمت چپ به بالای صفحه انتقال پیدا کرده)، فیلمهای موجود دوباره ضبط نشده و همین فیلمها قابل استفاده هستند.
مدت زمان آموزش: 47 دقیقه
محتویات درس: فیلم آموزشی
حجم فایل: 96 مگابایت
پیش نمایش جلسه ششم:
جلسه هفتم: تعریف متغیرهای ماتریسی و قیدها با استفاده از تولباکس یالمیپ
در این جلسه ابتدا نحوه تعریف متغیرهای ماتریسی با مثالهای متنوع در محیط متلب توضیح داده شده و سپس چگونگی تعریف قیدها یا همان ناتساویهای ماتریسی جهت استفاده در YALMIP با چندین مثال تشریح میشود.
مدت زمان آموزش: 62 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 85 مگابایت
پیش نمایش جلسه هفتم:
جلسه هشتم: تعریف تابع هزینه و حل LMI با استفاده از تولباکس یالمیپ
در این جلسه نحوه تعریف تابع هزینه، گزینه های اختیاری مربوط به YALMIP (به جز solver ها)، چگونگی حل مساله و در نهایت روش استخراج متغیرهای ماتریسی تشریح شده و مثال تحلیل پایداری که جلسات پیش با تولباکس متلب حل شده بود، با YALMIP هم حل میشود.
مدت زمان آموزش: 71 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 114 مگابایت
پیش نمایش جلسه هشتم:
جلسه نهم: معرفی و تشریح نحوه دانلود و نصب سه solver پرکاربرد به نامهای PENBMI ، SDPT3 و MOSEK
مباحث باقیمانده از توضیحات مربوط به YALMIP از جمله solver ها (داخلی و خارجی) در این جلسه مورد بحث قرار میگیرد. به طور خاص نحوه دانلود و نصب سه solver پرکاربرد به نامهای PENBMI ، SDPT3 و MOSEK به طور کامل تشریح شده و مثال تحلیل پایداری سیستم خطی که در جلسات قبل با تولباکس متلب حل شده بود، با این سه solver نیز حل میگردند.
مدت زمان آموزش: 73 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کد مثالهای نوشته شده در این جلسه
حجم فایل: 169 مگابایت
پیش نمایش جلسه نهم:
جلسه دهم: معرفی دینامیک غیرخطی قطار مغناطیسی شناور و خطیسازی حول نقطه کار
در این جلسه تکنولوژیهای موجود در ساخت قطارهای مغناطیسی معرفی شده و دینامیک غیرخطی شناورسازی یک قطار مغناطیسی با تکنولوژی EMS از یک مقاله IEEE ارایه میشود. در ادامه نقاط تعادل و نامی دینامیک استخراج شده و حول نقطه مورد نظر خطیسازی ژاکوبی انجام میشود تا ماتریسهای مورد نیاز برای طراحی کنترلکننده فیدبک حالت بدست آورده شود.
مدت زمان آموزش: 66 دقیقه
محتویات درس: فیلم آموزشی و کلیپی کوتاه از عملکرد قطار مغناطیسی- فایل پاورپوینت و مقاله IEEE حاوی دینامیک شناورسازی قطار مغناطیسی
حجم فایل: 116 مگابایت
پیش نمایش جلسه دهم:
جلسه یازدهم: طراحی و شبیهسازی فیدبک حالت برای سیستم شناور مغناطیسی
در این جلسه ابتدا دینامیک غیرخطی شناور مغناطیسی در محیط متلب و در نقطه کار دلخواه خطی شده و سپس با هر دو روش تولباکس LMI متلب و YALMIP مساله پایدارسازی سیستم خطی شده با فیدبک حالت حل میشود. همچنین بعد از بدست آوردن بهره کنترل کننده با استفاده از solver های PENBMI، SDPT3 و MOSEK در محیط YALMIP و بهره بدست آمده از تولباکس متلب، سیستم حلقه بسته (با دینامیک غیرخطی) در محیط سیمولینک شبیه سازی شده و نتایج حاصل از این بهره ها باهم مقایسه شده است.
مدت زمان آموزش: 67 دقیقه
محتویات درس: فیلم آموزشی- فایل پاورپوینت و کدها و فایلهای شبیه سازی سیستم حلقه بسته
حجم فایل: 113 مگابایت
پیش نمایش جلسه یازدهم:
مطالعه بیشتر
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم


Sadegh
سلام مجدد، من همون هستم که کامنت قبلی سوال پرسیدم!
ببخشید باز یک سوال دیگه دارم، این روش های LMI معمولا نهایتا در کنترل یا estimation به حل یک مساله LMIدر هر step از شبیه سازی منجر میشن، در این روش ها ماتریس هایی که داریم همگی از ابعاد کوچک هستند مثلا از ابعاد system order یا ابعاد کوچک زیر 20 یا 30 هستند.
مساله ی که من دارم در اصل ابعاد ماتریس ها و بردارها وابسته به کل دیتا ها هست، فرض کنید کلا دیتاهای ورودی خروجی سیستم در یک آزمایش، مثلا ممکنه این بردارها و ماتریس ها از بعد هزار در هزار یا حتی بیشتر باشند، و به همین شکل قید ها هم میتونن تعدادشون هزار عدد بشن! میتونم ازتون بپرسم آیا lmi میتونه اینکار رو انجام و در مقالات این روش متداول هست؟
ممنون میشم اگر راهنماییم کنید.
مرسی
علی جوادی
سلام
باید محدودیتهای متلب در حل LMI با ابعاد بالا رو ببینید. تا حالا برای من همچین موردی پیش نیومده
Sadegh
سلام، وقت شما بخیر، من سوالی دارم که جوابش در هیچکدام از این تیترها نیست،چونکه بیشتر آموزش مربوط به کنترل و مسایل طراحی کنترلر و رویتگر هست در این آموزش.
فرض کنید که من یک تابع هزینه Least squares دارم ولی این تابع هزینه homogeneous است، یعنی حداقل سازی نرم A*X این مساله رو میخوام با LMI حل کنم، ولی LMI جواب بدیهی X=0 را ایجاد می کند، در حالت حل آنالیزی ما قید: نرم x مساوی با یک را قرار می دهیم و مساله با SVD حل می شود، ولی این مساله را می خواهم با LMI حل کنم طوری که جواب بدیهی به من ندهد. اگر ممکن هست من رو راهنمایی کنید، و حتی اگر در ویدیوها هست بگید من تهیه میکنم.
با تشکر.
علی جوادی
سلام
من در این زمینه اطلاعی ندارم. باید به مقالات و کتابهای مربوطه مراجعه کنید
z
سلام
جلسه هفت پاورپوینت ندارد
علی جوادی
سلام
بنده همین الان چک کردم و فایل پاورپوینت داخل فایل دانلودی وجود داره.
احمد
سلام
اگر میشه موزیک ÷س زمینه را حذف کنید از فیلم
ممنون
علی جوادی
سلام
آهنگ پس زمینه فقط در پیش نمایشها وجود داره و اگر مجموعه رو تهیه و دانلود کنید هیچ کدام از جلسات آهنگ پس زمینه نداره
محمد
عرض سلام
من یه سوالی در مورد نحوه تعریف LMI سیستم های گسسته داشتم که آیا با پیوسته فرقی میکنه یا همون دستوراته ؟
با تشکر
علی جوادی
سلام
بله متفاوته چون فرمولبندی قانون پایداری لیاپونوف برای حالت پیوسته و گسسته فرق میکنند
محمد
با سلام
بنده یه سوال در مورد تعریف قسمت قید ها تو یالمیپ داشتم ، اگر قید ها به صورت LMI هایی بودند که داخل یه ماتریس تعریف شدند مثلاً یه ماتریس 3*3 اونموقع چطوری باید تو یالمیپ تعریفشون کرد ؟
با تشکر
علی جوادی
سلام
همه قیدها رو میتونید تعریف کنید حتی اگر تو در تو باشند
علی
سلام آقای دکتر
BRL رو هم در این مجموعه توضیح داده اید که چی هست و جهت تضعیف ورودی های مزاحم چگونه استفاده می شود؟
علی جوادی
سلام
خیر
علی
آقای دکتر
مبحث BRL در LMI در کدام یک از آموزش های شما توضیح داده شده است؟
علی جوادی
هیچکدام
مهران
سلام ممنون از تدریس عالی شما، من مجموعه رو کامل نگاه کردم ولی در حل یک ناتساوی ماتریسی به مشکل برخوردم که هیچ کدام از اون روش ها پاسخگوش نیستن، یعنی minimization براساس ترکیبی از متغیر های تصمیم گیری ما نیست بلکه به صورت زیر می باشد:
minimize K
0>[subject to [K*eye,P*B-B*Phat;B’*P-Phat*B’,K*eye
میشه راهنمایی کنید چجوری حل میشه؟
علی جوادی
سلام
اگر K جزو متغیرهای تصمیم گیری نیست، میتونید دستی مقدار کوچکی برای K تعیین کنید و ببینید نامساوی برقرار هست یا نه. اگر برقرار بود K رو کم کنید و ادامه بدید و اگر برقرار نبود K رو بیشتر کنیدو ادامه بدید.
فاطمه
سلام
ممنون از اموزش خوبتون
من میخوام حل به صورت دستی این LMI ها رو انجام بدم ممنون میشم راهنمایی بفرمایید.
علی جوادی
با سلام و تشکر از لطف شما
اگر منظورتون اینه که از تولباکسها نمیخواهید استفاده کنید و دوست دارید به صورت تحلیلی نامساویها رو حل کنید، این مجموعه بدرد شما نمیخوره.
در این مجموعه صرفا نحوه حل عددی نامساویها با استفاده از تولباکسهای متلب و یالمیپ تشریح شده
علیرضا
سلام آقای دکتر
سوالی داشتم خدمتون :برای یک سیستم که LPV هستش چه حلگری پیشنهاد می کنید چون تا الان از cvx و yalmip و … استفاده کردم که متاسفانه نه فیزیبل می شود و نه پایدار. به نظرتون مشکل از حلگر هستش یا LMI رو درست وارد نکردم. لطفا به ایمیلم پاسخ بدید . با تشکر…
علی جوادی
سلام
بابت تاخیر عذرخواهی میکنم اینترنت امروز وصل شد.
شما اول با تولباکس متلب امتحان کنید اگر فیزبل نشد یعنی یا LMI درست نیست یا کدها درست وارد نشده یا پارامترها تنظیم نشده و …
در کل برای اکثر مسایل اگر LMI ها با تولباکس متلب قابل حل باشند، با یالمیپ و cvx هم قابل حل هستند