فیلمهای مربوط به کنترل مقاوم فیدبک حالت سیستمهای خطی تحت اغتشاش و همچنین کنترل فیدبک خروجی سیستمهای خطی با استفاده از رویتگر قبلا خدمت دوستان تقدیم شده است. اگر سیستمی هم تحت تاثیر اغتشاش خارجی بوده و هم امکان اندازهگیری تمامی حالتها وجود نداشته باشد، دیگر نمیتوان از این فیلمها برای چنین سیستمی استفاده کرد. در سری فیلمهای حاضر دقیقا این مشکل مدنظر قرار گرفته و هدف طراحی یک کنترلکننده مقاوم برای سیستمهای خطی تحت تاثیر اغتشاش فقط با استفاده از یک یا چند خروجی سیستم است. کنترل کننده مورد نظر دارای رویتگر نبوده ولی دارای دینامیک داخلی است. همچنین تنها از خروجی سیستم فیدبک گرفته شده و نیازی به ورودی سیستم تحت کنترل ندارد. معیار تضعیف اغتشاش همان نرم ∞H است که به تفصیل در سری فیلمهای کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی تشریح شده و ارتباط آن با تلف کنندگی (Dissipativity) و پایداری بهره L2 بحث شده است. برای اطلاعات بیشتر در مورد تضعیف اغتشاش از طریق نرم ∞H و مزایای فرمولبندی این مساله به شکل LMI به فیلمهای مربوط به کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی مراجعه کنید.
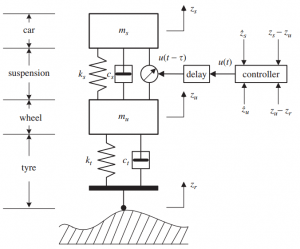
بعد از محاسبه نامساویهای ماتریسی خطی لازم برای حل مساله که ایده اصلی آن از یک مقاله IEEE گرفته شده است، روش پیشنهادی بر روی یک مدل یک چهارم سیستم تعلیق خودرو پیاده شده و سیستم حلقه بسته هم در محیط m-file و هم در سیمولینک شبیهسازی شده است. همچنین توابع تبدیل از نویز اندازه گیری، اغتشاش خارجی و ورودی مرجع به خروجی محاسبه شده و پهنای باند سیستم حلقه بسته و خواص تضعیف نویز و اغتشاش به صورت تحلیلی و شبیهسازی مورد بررسی قرار گرفته است. لازم به ذکر است که سیستم تعلیق در این سری فیلمها فقط به عنوان یک مثال کاربردی مورد استفاده قرار گرفته است و توضیح اضافی در مورد آن ارائه نشده است. برای درک بهتر این مثال شاید بهتر باشد قبل از دیدن این سری فیلمها، جلسات مربوط به مدلسازی و شبیهسازی ارتعاشات جاده برای سیستم کنترل تعلیق فعال خودرو را ملاحظه کنید و بعد از اینکه با سیستم تعلیق آشنا شدید، این سری فیلمها را ببینید.
با امید به اینکه مورد رضایت شما عزیزان قرار بگیرد
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
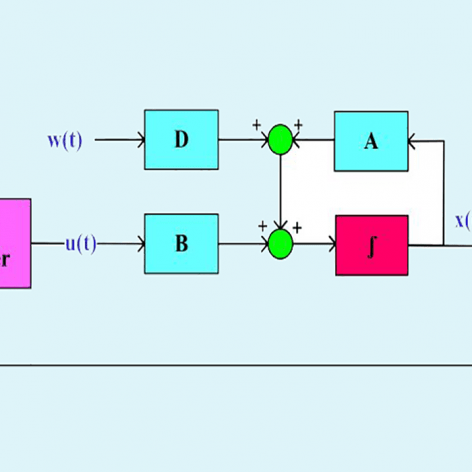
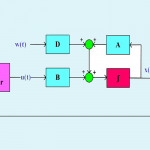
فرمولبندی طراحی کنترل مقاوم فیدبک خروجی برای سیستمهای دارای اغتشاش خارجی
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
پیادهسازی کنترلکننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیهسازی در متلب
شبیهسازی در محیط سیمولینک و تحلیل در حوزه فرکانس
جلسه دوم:
جلسه سوم:
جلسه چهارم:
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



الیاس
سلام آقای دکتر. خسته نباشید. ممنون از آموزش های خوبتان.
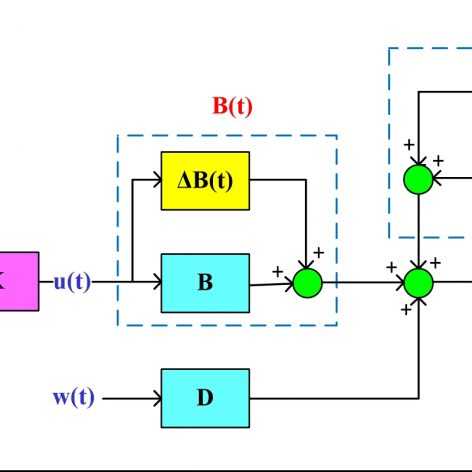
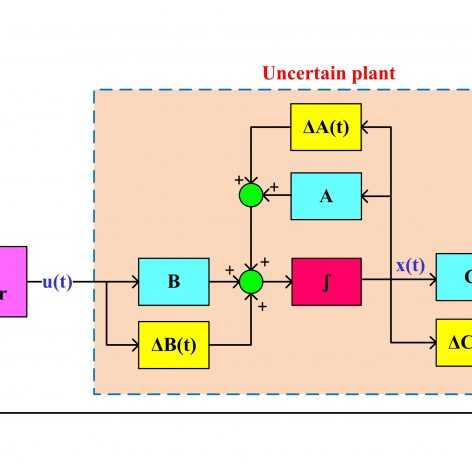
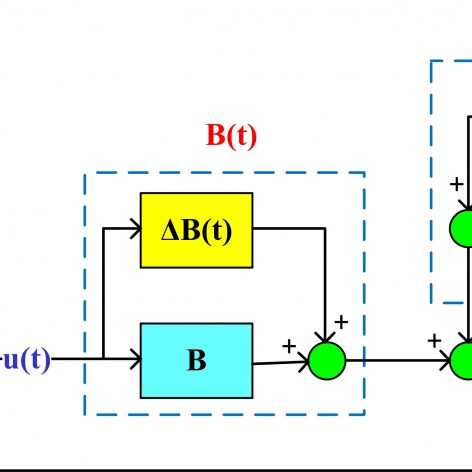
اگر LMI ای داشته باشیم که نسبت به ماتریس های سیستم آفین نباشد. مثلا ترم A.B داشته باشد. حال اگر این دو ماتریس نامعینی نرم محدود داشته باشند، آیا امکانش هست به صورت (A+dA)*(B+dB) نوشته شود و سپس به LMI تبدیل شود؟
اگر جوابتان بله است، امکانش هست در مورد ضرب ترم های نامعینی دار راهنمایی بفرمایید یا اگر مرجعی سراغ دارید، اعلام بفرمایید.
سپاسگزار از زحمات شما استاد گرامی
علی جوادی
با سلام و تشکر از لطف شما
من تا حالا به چنین موردی برخورد نکردم و نمیدونم چطور میشه به LMI تبدیل کرد
محمد
سلام و روز بخیر خدمت شما دکتر جوادی ببخشید بنظرتون امکان پذیره که کنترل h2 رو با مد لغزشی ترکیب کنیم؟؟؟
علی جوادی
سلام
من کار نکردم ولی ظاهرا امکانش هست:
https://www.researchgate.net/publication/261478970_A_sliding_mode_controller_with_generalized_H2_performance_for_dynamic_of_nonholonomic_mobile_robot
MOSLEH
با سلام
بنده قصد شبیه سازی مقاله ای که در حوزه کنترل مقاوم است رو دارم. عنوان این مقاله:
Robust Frequency Control in an Islanded Microgrid H∞ and μ-Synthesis Approaches
خواستم که در صورت امکان بفرمایید کدام یک از فایل های آموزشی شما توضیحات کاملی در خصوص این مطلب ارائه دادن؟
سپاسگزارم
علی جوادی
سلام
این مقاله از روش کلاسیک کنترل مقاوم (کنترل H-infinity و سنتز میو) استفاده کرده که من داخل هیچ جلسه ای اشاره ای بهش نکردم.
رویکرد من بر اساس LMI بوده و هیچ جلسه ای بدرد شما نمیخوره.
بهترین کار مطالعه کتابهای موجود کنترل مقاوم مثل کتاب دکتر تقی راد هستش.
فریبا
با سلام .ممنون از آموزش عالیتون.یه سوال داشتم از خدمتتون .فقط چون روابط زیاد داره امکان داره ایمیلتون رو داشته باشم ؟با تشکر
علی جوادی
با سلام و تشکر از لطف شما
اقدام شد
احسان
با عرض سلام و خسته نباشید خدمت شما استاد محترم.
سوالی داشتم از خدمتتون.
نویز در حالت پسیو قرار ندارد چون در فیدبک قرار داده شده است.
آیا در حالت پسیو برای مشاهده خروجی،مگر نباید آنجا هم اندازه گیری کنیم؟
بنابراین در پسیو هم مگر نباید مانند اکتیو تحت تاثیر نویز قرار گیرد؟
با سپاس از زحمات شما
علی جوادی
سلام
در حالت پسیو اصلا فیدبکی (و در نتیجه اندازهگیری) وجود ندارد که نویز اندازهگیری وجود داشته باشد.
در حالت پسیو سیستم حلقه باز کار میکنه
الیاس
سلام آقای دکتر. خسته نباشید.
سوالی داشتم از خدمتتون.
آیا فیدبک خروجی استاتیکی و یا فیدبک حالت دینامیکی هم کاربرد دارند؟
با تشکر فراوان
علی جوادی
سلام
اگر سیستم کنترل پذیر خروجی باشه فیدبک خروجی استاتیک میتونه مفید باشه.
منظورتون از فیدبک حالت دینامیکی رو متوجه نشدم
الیاس
ابتدا باید تشکر کنم بابت حسن توجه شما.
منظور سوالم این است که اگر در سیستمی تمام حالت ها در دسترس باشند، باز هم آیا نیاز است که از فیدبک دینامیکی استفاده کنیم؟
با تشکر از زحمات شما
علی جوادی
اگر همه حالتها در دسترس باشند، فیدبک دینامیکی چه کاربردی داره؟
حالتها کل رفتار داخلی سیستم رو توصیف می کنند و اگر در دسترس باشند نیازی به فیدبک دینامیکی نیست
الیاس
با عرض سلام و خسته نباشید خدمت استاد گرامی.
چرا وقتی پارامتر گاما را افزایش می دهیم، شکل های خروجی تقریبا می توان گفت تغییری نمی کند؟
مثلا به جای مقدار گاما=10، مقدار گاما=1000 را امتحان کردم، ولی تغییری در شکل ها ایجاد نشد.
با تشکر فراوان
علی جوادی
سلام
به خاطر اینکه وقتی گاما از یه حدی بیشتر میشه، اون قسمت از lmi که به گاما وابسته هست دیگه تاثیر زیادی روی برقراری کل نامساوی نداره.
بلحاظ فلسفی وقتی گاما رو زیاد انتخاب می کنید، یعنی شما تضعیف اغتشاش براتون خیلی مهم نیست و طبیعتا تغییر گاما روی نامساویها تاثیر زیادی نداره
الیاس
یک سوال کلی داشتم آقای دکتر.
فرض کنید ماتریس LMI ای داریم که چند ثابت طراحی در آن قرار دارد.
آیا در حالت کلی قبل از اجرای شبیه سازی می توان با تغییر پارامترها برآورد کرد که ناحیه شدنی بیشتر می شود یا اصلا جواب، ناشدنی می شود؟
در حالت کلی، ما یک ماتریس LMI می بینیم که یالمیپ دارد آن را optimize می کند و چیزی از داخل آن نمی دانیم. به نظر شما چگونه می توان به درک بهتر از این موضوع رسید؟
با تشکر فراروان از شما استاد گرامی
علی جوادی
بستگی به مفهوم اون پارامترهای طراحی داره.
در حالت کلی نمیشه قبل از حل LMI اظهار نظر کرد مگر اینکه بدونیم پارامترها چه اثری دارند
الیاس
سلام آقای دکتر. وقت شما بخیر
عذرخواهم سوالی داشتم از خدمتتون
آیا در LMI ای که در جلسه 2 همین بخش به دست آوردید، نمی شود بر روی آرایه 2-2 (منفی سیگما به توان 2) schur complement زد، تا خود سالور سیگمای بهینه را به دست آورد؟
در نهایت باید از تدریس خوبتان تشکر کنم و روز استاد را هم خدمتتان تبریک عرض می نمایم.
با تشکر
علی جوادی
سلام و وقت به خیر
فکر کنم منظورتون گاما باشه چون تو این LMI سیگما نداریم.
لازم به مکمل شور نیست شما میتونید گاما به توان 2 رو یک متغیر جدید تعریف کنید مثلا eta و بعد eta رو مینیمم کنید چون اگر eta مینیمم بشه گاما هم مینیمم میشه.
من این روش رو پیشنهاد نمیدم چون قبلا این کار رو کردم و جواب خوبی نگرفتم. ظاهرا علتش اینه که سالورهای تولباکس یالمیپ مسایل feasibility رو بهتر از مسایل مینیمم سازی حل می کنند.
بنابراین توصیه میکنم شما هم دستی گاما رو مینیمم کنید.
الیاس
خیلی ممنونم.
پس آیا می توان گفت برای مسایل مینیمم سازی بهتر است از تولباکس LMI خود متلب استفاده کنیم؟یا آن هم همین مشکل را دارد؟
سوال دیگری هم داشتم آقای دکتر، اگر با نامساوی ای به صورت زیر برخورد کنیم:
(X-Y’ZY<0) و Z هم ماتریسی مثبت باشد.
آیا باز هم از لم شور می توان استفاده کرد؟
(با توجه به این که زمانی که نامساوی کوچکتر از صفر باشد، در لم شور، درایه 2-2 آن باید منفی باشد.ولی در این حالت ماتریسی مثبت ((Z^(-1+) قرار می گیرد.)
با سپاس
علی جوادی
من با تولباکس متلب تا حالا تست نکردم خودتون میتونید امتحان کنید.
اگر X منفی معین باشه میشه از مکمل شور استفاده کرد و علامت منفی مهم نیست.
لطفا به صفحه ویکیپدیای مکمل شور مراجعه کنید:
https://en.wikipedia.org/wiki/Schur_complement
احسان
سلام آقای دکتر. وقت شما بخیر. ابتدا باید تشکر کنم از زحمات شما استاد گرامی. سپس سوالی داشتم از خدمتتون.
کتاب یا مقاله هایی که LMI های به دست آمده در آن باشد را (برای ارجاع دادن) می توانید معرفی کنید.
(در صورت امکان برای سری آموزش های دیگر کنترل مقاوم هم معرفی نمایید.)
با تشکر فراوان از شما استاد گرامی
علی جوادی
با سلام و تشکر از لطف شما
این lmi ها رو خودم استخراج کردم و به صورت آماده که می بینید در مرجعی ندیدم (البته شاید جایی موجود باشه و من ندیده باشم). میتونید به همون مراجعی که در فیلمها اشاره شده ارجاع بدید. البته مقاله خودم ارسال شده ولی هنوز چاپ نشده و هر وقت چاپ شد اطلاع رسانی میکنم تا بهش ارجاع بدید.
موفق باشید
احسان
ممنون میشم اگر در کانال تلگرام اطلاع رسانی نمایید.
وجود شما برای رشته کنترل، نعمت بزرگی به حساب می آید.
با تشکر فراوان.
علی جوادی
اگر خاطرم بود حتما
ابوالفضل
با سلام و عرض ادب و تشکر فراوان بخاطر آموزش بسیار خوبتون.
جناب دکتر بنده بروی مقاله ای کار میکنم که پایه و اساس پایان نامه من منطبق با اون هستش.
حالت های سیستم به دست آومده معادل یک ماتریس 4*4 =A و ماتریس 2*4=B و ماتریس 4*2=C هستند.
مشکلی که نتونستم راه حلی براش پیدا کنم اینکه داخل ماتریس A، پارامترهای ماتریس وابسته به حالتهای سیستم هستن. یعنی در ابتدا ثابت نیستن مثل مثالهای که واسه نمونه حل کریدن.
ممنون میشم راهنمایی کنید که چطور بتونم کد نویسی این حالت از سیستم انجام بدم.
علی جوادی
با سلام و تشکر از لطف شما
با توضیحاتی که دادید، سیستم شما غیرخطی بوده و از روشهای موجود در این سری فیلمها نمیشه استفاده کرد.
باید از روشهای مقاوم غیرخطی مثل مد لغزشی استفاده کنید