فیلمهای مربوط به کنترل مقاوم فیدبک حالت سیستمهای خطی تحت اغتشاش و همچنین کنترل فیدبک خروجی سیستمهای خطی با استفاده از رویتگر قبلا خدمت دوستان تقدیم شده است. اگر سیستمی هم تحت تاثیر اغتشاش خارجی بوده و هم امکان اندازهگیری تمامی حالتها وجود نداشته باشد، دیگر نمیتوان از این فیلمها برای چنین سیستمی استفاده کرد. در سری فیلمهای حاضر دقیقا این مشکل مدنظر قرار گرفته و هدف طراحی یک کنترلکننده مقاوم برای سیستمهای خطی تحت تاثیر اغتشاش فقط با استفاده از یک یا چند خروجی سیستم است. کنترل کننده مورد نظر دارای رویتگر نبوده ولی دارای دینامیک داخلی است. همچنین تنها از خروجی سیستم فیدبک گرفته شده و نیازی به ورودی سیستم تحت کنترل ندارد. معیار تضعیف اغتشاش همان نرم ∞H است که به تفصیل در سری فیلمهای کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی تشریح شده و ارتباط آن با تلف کنندگی (Dissipativity) و پایداری بهره L2 بحث شده است. برای اطلاعات بیشتر در مورد تضعیف اغتشاش از طریق نرم ∞H و مزایای فرمولبندی این مساله به شکل LMI به فیلمهای مربوط به کنترل مقاوم سیستمهای خطی تحت اغتشاش با استفاده از نامساویهای خطی ماتریسی مراجعه کنید.
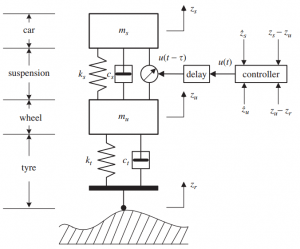
بعد از محاسبه نامساویهای ماتریسی خطی لازم برای حل مساله که ایده اصلی آن از یک مقاله IEEE گرفته شده است، روش پیشنهادی بر روی یک مدل یک چهارم سیستم تعلیق خودرو پیاده شده و سیستم حلقه بسته هم در محیط m-file و هم در سیمولینک شبیهسازی شده است. همچنین توابع تبدیل از نویز اندازه گیری، اغتشاش خارجی و ورودی مرجع به خروجی محاسبه شده و پهنای باند سیستم حلقه بسته و خواص تضعیف نویز و اغتشاش به صورت تحلیلی و شبیهسازی مورد بررسی قرار گرفته است. لازم به ذکر است که سیستم تعلیق در این سری فیلمها فقط به عنوان یک مثال کاربردی مورد استفاده قرار گرفته است و توضیح اضافی در مورد آن ارائه نشده است. برای درک بهتر این مثال شاید بهتر باشد قبل از دیدن این سری فیلمها، جلسات مربوط به مدلسازی و شبیهسازی ارتعاشات جاده برای سیستم کنترل تعلیق فعال خودرو را ملاحظه کنید و بعد از اینکه با سیستم تعلیق آشنا شدید، این سری فیلمها را ببینید.
با امید به اینکه مورد رضایت شما عزیزان قرار بگیرد
پیشنیازها: آشنایی اولیه با جبر خطی و تئوری پایداری لیاپونوف – آشنایی با کدنویسی در محیط متلب – آشنایی با نامساویهای ماتریسی خطی (LMI)
قبل از دیدن ادامه پست، راهنمای استفاده از سری فیلمهای کنترل مقاوم را حتما ببینید:
جلسه اول:
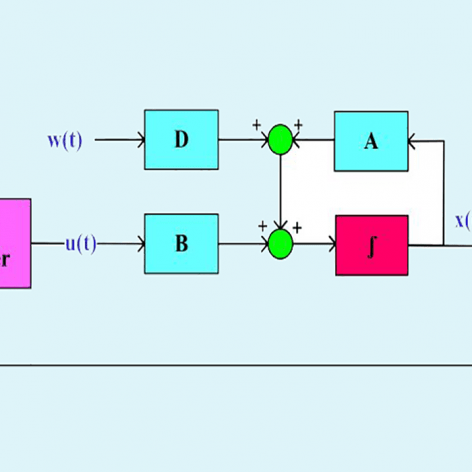
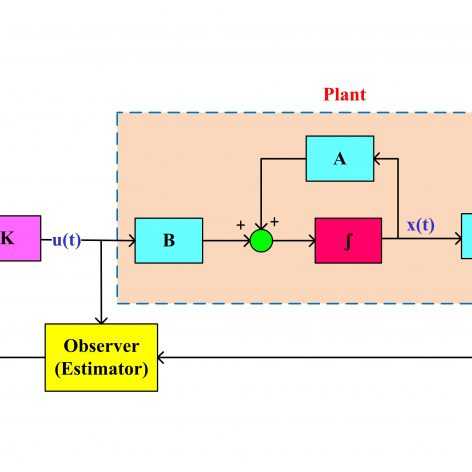
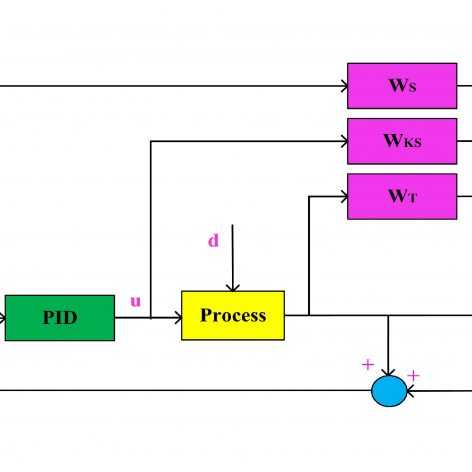
فرمولبندی طراحی کنترل مقاوم فیدبک خروجی برای سیستمهای دارای اغتشاش خارجی
استخراج LMI های مورد نیاز با استفاده از مکمل شور و تبدیل متجانس
پیادهسازی کنترلکننده مقاوم بر روی سیستم تعلیق فعال خودرو و شبیهسازی در متلب
شبیهسازی در محیط سیمولینک و تحلیل در حوزه فرکانس
جلسه دوم:
جلسه سوم:
جلسه چهارم:
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم



فرزاد
با سلام و احترام، روش کنترلی چرا برای زمانی که ماتریس B از یک ستون بیشتر است. اجرا نمیشود؟ و اخطار می دهد که ابعاد ماتریس درست نیست؟
علی جوادی
احتمالا کد برای سیستمهای تک ورودی نوشته شده.
ابعاد ماتریسها رو با توجه به تعداد ورودیها اصلاح کنید.
احسان
سلام آقای دکتر. وقت شما بخیر.
سوالی داشتم از خدمتتون.
ما LMI ای داریم، که یک متغیر اسکالر در ماتریس متغیرهای تصمیم گیری ضرب شده است و با توجه به تغییر آن اسکالر، مقدار گاما «شاخص Hinf» خیلی تغییر می کند. باتوجه به این که در این حالت مشابه فیلم های آموزشی، متغیر اسکالر را دستی باید مشخص کنیم، با حل کردن LMI ها، آیا می توان از روش های بهینه سازی هوشمند یا هر روش دیگر، آن اسکالر را مشخص نمود به طوری که گاما کمینه شود؟
با تشکر از زحمات شما
علی جوادی
بهترین راه تنظیم دستی گاماست در غیر اینصورت ممکنه مقدار مناسبی بدست نیاد
سعید
سلام
مدل بد ست امده ازیک سیستم برای استفاده در روش پیشنهادی باید گسسته باشد یا پیوسته؟
علی جوادی
سلام
مدل پیوسته
فرزاد
با سلام
من برنامه رو اجرا می کنم بخش دومشو که متغیرهای کنترل کننده رو پیدا میکنه این اخطارو میده ممنون میشم راهنمایی کنین،یعنی نیاز یالمیپو نصب شه؟
Undefined function or variable ‘sdpvar’
علی جوادی
سلام
بله باید یالمیپ رو نصب کنید
فرزاد
با سلام و عرض خسته نباشید خدمت شما
روشی که در اموزشی ارائه کردین چه تفاوتی با مجموع کنترل H بی نهایت کلاسیک که در متلب موجود است، دارد
علی جوادی
سلام
تنها تفاوت در اینه که مساله به فرم LMI فرمولبندی شده و نحوه فرمولبندی مساله توضیح داده شده ولی در تولباکس آماده متلب صرفا مساله رو وارد میکنید و کنترل کننده تحویل داده میشه و اطلاع ندارید که مساله چطور حل شده
فرزاد
با سلام
ممنون از اموزش خوبی که ارائه کردین، خواستم بدونم روش پیشنهادی با روش H بی نهایت مقایسه شده؟
و آیا این روش بهتر است یا روش کنترل H بی نهایت، یا بستگی به نوع مسئله دارد که کدام بهتر عمل کند.با تشکر
علی جوادی
در این مجموعه تضعیف اغتشاش با استفاده از روش H بینهایت انجام شده و حذف نامعینی با روش دیگری که توضیح داده شده
ایمان
سلام آقای دکتر. وقت شما بخیر. عذرخواهم برای استفاده از فیدبک خروجی دینامیکی، نباید رویت پذیری یا آشکار پذیری را بررسی نماییم؟
مثلا ممکن است یک مدل سیستم، 6 حالت داشته باشد و فقط در خروجی یک حالت را داشته باشیم، آیا بازهم کنترل کننده فیدبک خروجی جواب می دهد؟ یا نیاز است شرطی را از قبل بررسی نماییم؟
با سپاس از زحمات شما
علی جوادی
سلام
در فیدبک خروجی هدف تخمین حالتها نیست بنابراین به نظر میرسه رویت پذیری در این حالت معنی نداشته باشه
جواد
با سلام و خسته نباشید.
خواستم ببینم این آموزش را تهیه کنیم نیاز به آموزش های قبلی که بطور جداگانه نامعینی های پارامتری و اغتشاش تدریس شده نخواهم داشت؟ آیا این آموزش ها مستقل هستند؟
سوال بعدی اینکه تئوری پایداری لیاپونوف را از کدوم فیلم آموزشی استفاده کنیم؟
ممنون
علی جوادی
سلام
برای درک کامل مطالب ارائه شده بهتره آموزشهای قبلی رو به ترتیب انتشار ببینید. مثلا مدلسازی نامعینی پارامتری در مجموعه های قبلی گفته شده.
اما اگر صرفا هدفتون حل LMI های بدست اومده برای سیستم خودتون باشه همین مجموعه کفایت میکنه.
تئوری لیاپونوف هم تقریبا در همه مجموعه های مقاوم اشاره شده ولی خیلی مفصل مطرح نشده.
احسان
سلام آقای دکتر. خسته نباشید. ابتدا باید تشکر کنم بابت آموزش های بسیار خوبتان.
سوالی داشتم از خدمتتان. زمانی که
V(x(inf)) -V(x(0)) (1
را به نامساوی کنترل H inf اضافه می کنیم، ممکن است شرایط اولیه سیستم برابر با صفر نباشد، بنابراین
V(x(0)) (2
صفر نشود. این مساله را چگونه توجیه می کنید؟
با سپاس از زحمات شما
علی جوادی
سلام
برای اثبات روش H-inf باید شرایط اولیه را صفر در نظر بگیریم بنابراین باید اول بدون اغتشاش پایداری داخلی به شرایط اولیه اثبات بشه (که انجام شده) و بعد بحث تضعیف اغتشاش بدون شرایط اولیه مطرح شده. البته اگر نامساویهای H-inf برقرار باشه، اثبات میشه که پایداری داخلی نسبت به شرایط اولیه برقرار هست بنابراین در هر صورت مشکلی وجود نداره
محمد
سلام اقای دکتر روزتون بخیر ببخشید من تازه می خوام کنترل مقاوم شروع کنم از صفر بدون هیچ گونه اشنایی ببخشید ممنون میشم راهنماییم کنید از کدوم قسمت اموزش شروع کنم اخه چهار قسمت اموزش دارید من نمیدونم از کدوم قسمت شروع کنم هدف من یادگیری کنترل مقاوم وطراحی اون برای سیستم های غیر خطی هستش ممنون میشم راهنماییم کنید
علی جوادی
سلام
تمام روشهای مقاوم که توسط بنده در اینجا ارائه شده برای سیستمهای خطی قابل استفاده است.
برای سیستمهای غیرخطی از روشهای مقاوم دیگه مثل مدلغزشی استفاده کنید که داخل سایت موجود هست.
محمد
خب ببخشید ی سوال داشتم اقای دکتر یعنی نمیشه از روش کنترل مقاوم به منظور طراحی کنترل کننده برای سیستم هایغیر خطی استفاده کرد سیستم تعلیق هم مدل غیر خطی داره یعنی ببخشید حتما باید خطی سازی بشه با lmi بعد کنترل کننده اعمال بشه
علی جوادی
روشهایی که من گفتم خطی هستند وگرنه روشهایی دیگری برای کنترل مقاوم سیستمهای غیرخطی وجود دارند مثل مدلغزشی
محمد
جناب اقای دکتر جوادی عزیز ببخشید منظورم بد رسوندم خدمتتون ببخشیدیعنی نمیشه از روش h2 یا hinf برای بررسی سیستم های غیر خطی بدون خطی سازی lmi استفاده کرد؟؟
علی جوادی
برای سیستمهای غیرخطی هم میشه از روش Hinfinity استفاده کرد ولی من در فیلمهای ارائه شده در سایت اشاره نکردم.
مثلا به کتاب زیر میتونید مراجعه کنید:
https://www.oreilly.com/library/view/nonlinear-h-infinity-control/9781439854853/