در این جلسه سیستم کوادروتور از لحاظ سخت افزاری و عملکردی به طور کامل توضیح داده می شود. این جلسه تحت عنوان پیش درامدی بر کوادروتور ارایه می شود.
مدت زمان: 70 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
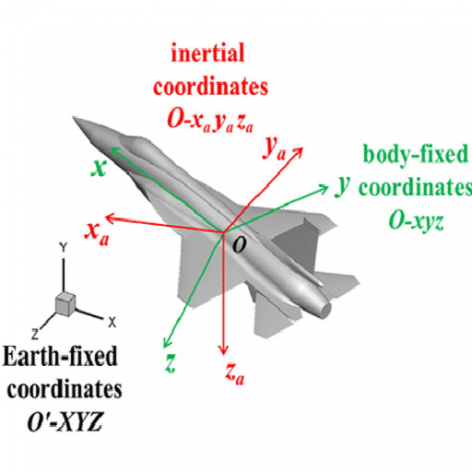
در این جلسه مفهوم پایه ای عملکرد سیستم کوادروتور، معرفی محورهای فرضی حاکم بر سیستم، نحوه انتقال از فریم بدنه به فریم اینرسایی و بالعکس و همچنین نحوه استخراج معادلات دینامیکی موتورهای براشلس DC مورد استفاده در سیستم کوادروتور به طور کامل توضیح داده می شود. . این جلسه تحت عنوان مدلسازی سیستم کوادروتور بخش (1) ارایه می شود.
مدت زمان: 52 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
در این جلسه مدل ریاضی کوادروتور شامل متغیرهای حالت سیستم به طور کامل بررسی می شود. در ادامه معادلات دینامیکی حاکم بر سیستم کوادروتور از طریق دو روش نیوتن-اویلر و همچنین اویلر-لاگرانژ به صورت جداگانه و به تفصیل توضیح داده می شود. این جلسه تحت عنوان مدلسازی سیستم کوادروتور بخش (2) ارایه می شود.
مدت زمان: 53 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
در این جلسه مدل ریاضی سیستم کوادروتور از منظری دیگر مورد بررسی قرار می گیرد و مدلسازی سیستم کوادروتور بر مبنای تعاریف علم سینماتیک و علم دینامیک انجام و معادلات ریاضی سیستم استخراج می گردد . در ادامه نیروها و گشتاورهای وارد بر سیستم کوادروتور به طور کامل توضیح داده می شوند و در نهایت نحوه به دست اوردن معادلات فضای حالت سیستم شرح داده می شود. این جلسه تحت عنوان مدلسازی سیستم کوادروتور بخش (3) ارایه می شود.
مدت زمان: 52 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
در این جلسه به علم ایرودینامیک پرواز پرداخته می شود. نیروهای ایرودینامیکی به طور کامل توضیح داده می شوند و سپس ایرودینامیک عمودپروازها به طور اختصاصی برای سیستم کوادروتور مطرح و روابط ان استخراج می گردد. در ادامه نحوه محاسبه سرعت و مسیر باد که مهمترین عامل اغتشاش خارجی بر هم زننده تعادل این سیستم پرنده می باشد، مطرح می گردد. این جلسه تحت عنوان ایرودینامیک پرواز (1) ارایه می شود.
مدت زمان: 70 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
این جلسه در ادامه جلسه پنجم ، به تکمیل روابط ریاضی ایرودینامیک پرواز سیستم کوادروتور می پردازد. در ادامه روش های محاسبه نیروی دراگ جهت تخمین بردار و مسیر باد به طور کامل شرح داده می شوند و در نهایت معادلات فضای حالت سیستم کوادروتور به همراه اثرات ایرودینامیکی استخراج می گردند. این جلسه تحت عنوان ایرودینامیک پرواز (2) ارایه می شود.
مدت زمان: 50 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
در این جلسه به ساختار کنترلی سیستم کوادروتور پرداخته می شود و تمامی لایه های کنترلی به همراه بلوک دیاگرام انها و ارتباط بین هریک از این لایه های کنترلی به طور کامل مطرح می گردد . دانش کسب شده در این جلسه پیش زمینه طراحی هر نوع کنترلر دلخواه برای این سیستم پرنده می باشد.
مدت زمان: 66 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
در این جلسه فیلتر کالمن پیوسته توسعه یافته به عنوان یک مشاهده گر و تخمین زننده مطرح در سیستم های غیر خطی معرفی می گردد و در نهایت نحوه تخمین متغیرهای حالت سیستم کوادروتور بر مبنای این نوع فیلتر خاص به طور کامل توضیح داده می شود..
مدت زمان: 70 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس
کیفیت: 720P
در این جلسه نحوه پیاده سازی روش کنترلی مد لغزشی بر روی سیستم کوادروتور به صورت تیوری و به صورت شبیه سازی شده در نرم افزار متلب اموزش داده می شود.
مدت زمان: 72 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس ، m-file های نرم افزار متلب
کیفیت: 720P
در این جلسه نحوه پیاده سازی الگوریتم بهینه سازی ژنتیک به عنوان یک روش تحلیلی ، جهت محاسبه دقیق تری از پارامترهای کنترل کننده مد لغزشی اموزش داده می شود.
مدت زمان: 74 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس ، m-file های نرم افزار متلب
کیفیت: 720p
در این جلسه نحوه پیاده سازی فیلتر کالمن پیوسته توسعه یافته ، جهت تخمین متغیرهای حالت سیستم کوادروتور در نرم افزار متلب اموزش داده می شود.
مدت زمان: 47 دقیقه
فایل های همراه: فایل تصویری ، m-file های نرم افزار متلب
کیفیت: 720p
در این جلسه نحوه پیاده سازی کنترل کننده پسگام (Backstepping) ، بر روی سیستم کوادروتور به صورت تیوری و به صورت شبیه سازی شده در نرم افزار متلب اموزش داده می شود.
مدت زمان: 57 دقیقه
فایل های همراه: فایل تصویری ، پاورپوینت درس ، m-file های نرم افزار متلب
کیفیت: 720p
در این جلسه اموزشی ، نحوه پیاده سازی یک کنترل کننده مقاوم و بهینه ترکیبی(ROSMC) بر مبنای معادلات ریکاتی وابسته به حالت ( SDRE) تحت عنوان (Robust Optimal Sliding Mode Control based on SDRE) ، بر روی سیستم کوادروتور به صورت تیوری و به صورت شبیه سازی شده در نرم افزار متلب در چهار بخش جداگانه به صورت زیر اموزش داده می شود.
مدت زمان جلسه :4 ساعت و30 دقیقه
فایل های همراه جلسه: فایل تصویری ، فایل پاورپوینت درس ، ، m-file های نرم افزار متلب
بخش اول :
طراحی قانون کنترل بهینه مقاوم با استفاده از کنترل کننده مد لغزشی بر اساس معادلات
ریکاتی وابسته به حالت
مدت زمان بخش اول : 2 ساعت و 5 دقیقه
فایل های همراه بخش اول: فایل تصویری ، فایل پاورپوینت درس ، فایل PDF پاورپوینت درس
پیش نمایش جلسه اول
بخش دوم:
برنامه نویسی روش کنترلی Robust Optimal Sliding Mode based on SDRE
در حالت Point to Point
مدت زمان بخش دوم : 1 ساعت و 5 دقیقه
فایل های همراه بخش دوم: فایل تصویری ، فایل پاورپوینت درس ، m-file های نرم افزار متلب
پیش نمایش بخش دوم
بخش سوم :
برنامه نویسی روش کنترلی Robust Optimal Sliding Mode based on SDRE
در حالت Trajectory Tracking
مدت زمان بخش سوم : 35 دقیقه
فایل های همراه بخش سوم: فایل تصویری ، فایل پاورپوینت درس ، m-file های نرم افزار متلب
پیش نمایش بخش سوم
بخش چهارم :
برنامه نویسی روش کنترلی Robust Optimal Sliding Mode based on SDRE
جهت محاسبه خطای Minimum Mean Square Error
مدت زمان بخش چهارم 45 دقیقه
فایل های همراه بخش چهارم : فایل تصویری ، فایل پاورپوینت درس ، m-file های نرم افزار متلب
پیش نمایش بخش چهارم
در این جلسه اموزشی ، نحوه پیاده سازی کنترل کننده گام به عقب(Backstepping) به صورت ترکیب با فیلتر کالمن توسعه یافته پیوسته (Extended Kalman Bucy Filter) در حالت ردیابی یک مسیر از پیش تعیین شده (Trajectory Tracking) ، بر روی سیستم کوادروتور به صورت شبیه سازی شده در نرم افزار متلب اموزش داده می شود.
مدت زمان جلسه :45 دقیقه
فایل های همراه جلسه: فایل تصویری ، m-file های نرم افزار متلب
 مرجع مهندسی كنترل | دانش با کیفیت در مرز علم
مرجع مهندسی كنترل | دانش با کیفیت در مرز علم





مهران
سلام
تو کد SMC به یه ابهامی برخوردم
اگر phi_desired =80/180*pi و x_desired=30 و سایر پارامترهای مطلوب برابر صفر باشن، این کنترلر بدون هیچ مشکلی در نقطه مورد نظر قرار میگیره؟!
این مسئله چطور توجیه میشه؟
مهندس بابایی
سلام بر شما
زمانی که اغتشاش به سیستم هنوز اعمال نشده باشد، بله توجیه پذیر است. عدم وجود اغتشاش شرایط را برای تعیین پارامترهای بهینه برای ردیابی مسیر نقطه به نقطه یا حتی سینوسی بسیار هموار می سازدو هرچند که با وجود اغتشاش نیز، با بهرهگیری از روش های بهینه سازی در تعیین پارامترها باز هم می توان تا حدود زیادی به نتایج دلخواه دست یافت.
حسین
سلام وخسته نباشید خانم دکتر،
ببخشیداگر بخواهیم اغتشاش بار در کوادکوپتر، چگونه میشود در نظر گرفت ؟ مثلا امکانش هست که یه ضریبی به جرم کوادکوپتر اضافه کرد که با گذشت زمان کم میشود(هدف من این هست که مثلا باری داشته باشد که با گذشت زمان جرم بار کم میشود)؟ و با کنترل اسلایندیگمیشه این اغتشاش رو حذف کرد؟
ممنون میشم اگه مقاله ای در این زمینه دارید در اختیارم بذارین. چون مقالاتی که سرچ کردم چنین چیزی که جرم رو به عنوان اغتشاش در نظر بگیرد پیدا نکردم.
با تشکراز آموزش عالیتان
مهندس بابایی
سلام بر شما
من شخصا روی عدم قطعیت بار به صورت اغتشاش کار نکرده ام. حتما می بایست از مراجع موجود به عنوان رفرنس استفاده کنید. قطعا با روش های جستجویی که در دروس اموزش اسکوپوس، گوگل اسکالر، وب او ساینس خدمت شما دوستان ارایه کردم، مقالات و پایان نامه های بسیار زیادی در زمینه کاری که مطرح نمودبد، پیدا خواهید کرد.حتما از جستجوی پیشرفته استفاده نمایید.
موفق باشید.
حسین
سلام وخسته نباشید خانم دکتر
اگر این امکان وجود داشته باشه که شبیه سازی کوادروتور وقتی ماتریس اینرسی ها متغیرن یا وقتی مثلا جرم متغیری رو حمل میکنه،با روش اسلایدینگ یا بک استپینگ انجام بشه ممنون میشم.
یا اگر کلاس انلاین در این زمینه دارید میخواستم ثبت نام کنم.
ممنون از آموزش خوبتان
مهندس بابایی
سلام بر شما
متاسفانه در حال حاضر چنین کلاسی اموزشی در دست اجرا ندارم.
موفق باشید.
حسین
سلام خانم دکتر،وقتتون بخیر
ببخشید در جلسه دوازدهم،تو روش بک استپ، تو ام فایل در فضای حالت سیستم نوشتین
( x8(i+1)=x8(i)+dt*(-g+(((cos(x1(i))*cos(x3(i))*u1(i))/m ، در حالی که تو پاور پوینتها (x12(i+1 برابر این مقدار هستش. وقتی اینها رو تو ام فایل درستش میکنم کنترل کننده درست کار نمیکنن. نمیدونم مشکل کجاست.
با تشکر از آموزش عالیتان.
مهندس بابایی
سلام بر شما
این موضوع قبلا به کامنت دوستانتون و همچنین در جلسات اموزشی بعدی توضیح داده شده است. این تفاوت بدان علت است که شما متغیر z را بخواهید x7 تعریف کنید و یا x11.
که در نهایت هیچ فرقی نمی کند، فقط تعریف ان به طور صحیح مهم است که برابر با ( x8(i+1)=x8(i)+dt*(-g+(((cos(x1(i))*cos(x3(i))*u1(i))/m یا ( x12(i+1)=x12(i)+dt*(-g+(((cos(x1(i))*cos(x3(i))*u1(i))/m باشد.
از m-file هایی که شخصا برای شما قرار دادم استفاده نمایید و تغییری در ان ایجاد نکنید.
موفق باشید.
ali
با سلام
در بخش طراحی مدلغزشی شما شش S را حساب کردین و سپس از آنها مشتق گرفته و برابر (Ksgn(s مربوط به آن سطح لغزشی قرار دادین و U ها بدست آمد. دو سوال برایم پیش آمده است:
1.چرا؟ مگر نباید Sdot را مساوی صفر قرار میدادید؟
2.برای مدلغزشی مرتبه دو (فراپیچشی) با u=ueq-a|s|^p.sgn(s)-b.ant(sgn(s))dt آیا باید Sdot را مساوی a|s|^p.sgn(s)+b.ant(sgn(s))dt قرار دهیم یا (Ksgn(s ؟؟؟
مهندس بابایی
سلام بر شما
در رابطه با سوال اول شما : دقیقا Sdot ها برابر صفر قرار داده شده اند. در واقع (Ksgn(s معادل مشتق سطوح اسلایدها می باشد. لطفا اسلاید شماره 8-11 مربوط به پاورپوینت جلسه نهم و فیلم اموزشی ان را مجددا ملاحظه بفرمایید.
در رابطه با سوال دوم: این موضوع در این جلسات اموزشی تدریس نشده است. برای اطلاعات بیشتر می توانید به مقاله موجود از اینجانب و همچنین درس اموزش مد لغزشی مرتبه دوم که توسط همکاران ارایه شده است مراجعه بفرمایید.
موفق باشید.
ali
با سلام
در بخش طراحی مدلغزشی شما شش S را حساب کردین و سپس از آنها مشتق گرفته و برابر (Ksgn(s مربوط به آن سطح لغزشی قرار دادین و U ها بدست آمد. دو سوال
1.چرا؟ مگر نباید Sdot را مساوی صفر قرار میدادید؟
2.برای مدلغزشی مرتبه دو (فراپیچشی) با u=ueq-a|s|^p.sgn(s)-b.ant(sgn(s))dt آیا باید Sdot را مساوی a|s|^p.sgn(s)+b.ant(sgn(s))dt قرار دهیم یا (Ksgn(s ؟؟؟
هومن
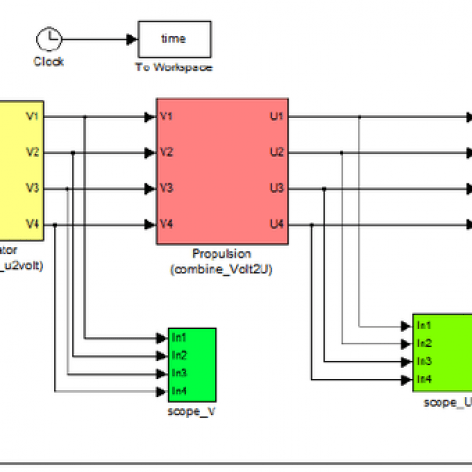
اگر این امکان وجود داشته باشه که شبیه سازی در محیط سیمولینک متلب با بلاک دیاگرام به طور مثال برای نمونه SMC انجام بشه ممنون میشم.
مهندس بابایی
متاسفانه به علت مشغله کاری فرصت کافی برای انجام این کار رو ندارم.
موفق باشید.
هومن
سلام
همانطوری که در جلساتتون فرمودید که بلاک دیاگرام مهم هستش پس چرا شما در هیچ یک از مقاله های که بیان کردید برای رفرنسدهی بلاک دیاگرام کنترلی قرار ندادید؟
مهندس بابایی
سلام بر شما
بله مهم هست اما گاهی بنا به دلایلی مثل محدود بودن صفحات ارایه مقاله، زیاد پیچیده نبودن فرایند کنترلی و یا عدم درخواست توسط داوران می توان از ارایه ان صرفه نظر نمود. اما باز هم تاکید می کنم اگر شخصا داوری مقاله ای را به عهده داشته باشم از نویسندگان ان مقاله این موضوع را خواستار خواهم شد.
موفق باشید.
هومن
سلام
در جلسه نهم در سیگنال های کنترلر اثر از اغتشاش خارجی نیست ممنون میشم توضیح بفرمایید. در مورد اغتشاش در جلسه ششم اشاره شده اما به نظر میرسه در جلسه نهم که طراحی SMC هستش درنظر گرفته نشده. لطف میفرمایید اگر راهنمایی کنید.
مهندس بابایی
سلام بر شما
بله توضیح دادم که خود دوستان اگر تمایل داشتند بدانند که چگونه باید ان را به سیستم اعمال کنند. اما برای یاداوری باز هم تکرار میکنم :
از همان قسمتی که ورودی به سیستم اعمال می شود می تونید یک اغتشاش خارجی که فرمت های متفاوتی هم می تونه داشته باشه به سیستم اعمال کنید. توصیه می کنم ابتدا دامنه اغتشاش رو پایین در نظر بگیرید و کم کم تا جایی که کنترل کننده توانایی حذف اون رو داره، دامنه و فرکانس رو افزایش بدید.
موفق باشید.
هومن
سلام، ممنون از آموزش خوبتون
چطوری میشه به مقاله هایی که براساس اونها توضیح داده شده رجوع کنم،
مقاله های مرتبط با هر فصل مورد نیاز هست که رجوع کنم به اونا ، از کجا میتونم داشته باشم؟
مهندس بابایی
سلام بر شما
می تونید به مقالات من که در زیر لینکشون رو براتون قرار دادم رجوع بفرمایید و به همون ها هم رفرنس دهی کنید.
در ادامه نیز من لینک برخی از مقالاتم رو براتون قرار میدم:
https://journals.sagepub.com/doi/full/10.1177/0142331216640600
https://ieeexplore.ieee.org/document/7985155
http://ijeee.iust.ac.ir/article-1-1258-en.html
https://miscj.aut.ac.ir/article_3113.html
http://psc-ir.com/cd/2016/papers/1421.pdf
پایدار باشید.